inlabru interface

Introduction

The excursions package can also be used to analyze results obtained using inlabru. An advantage with inlabru is that it usually simplifies the model specification compared with plain INLA. To analyze inlabru outputs, the functions excursions.inla, simconf.inla and contourmap.inla can be used. Let us illustrate this using simulated data.

Let us generate some data

n.lattice <- 30
x <- seq(from = 0, to = 10, length.out = n.lattice)
lattice <- fm_lattice_2d(x = x, y = x)
mesh <- fm_rcdt_2d_inla(lattice = lattice, extend = FALSE, refine = FALSE)

sigma2.e <- 0.1
n.obs <- 100
obs.loc <- cbind(
  runif(n.obs) * diff(range(x)) + min(x),
  runif(n.obs) * diff(range(x)) + min(x)
)
Q <- fm_matern_precision(mesh, alpha = 2, rho = 3, sigma = 1)
x <- fm_sample(n = 1, Q = Q)
A <- fm_basis(mesh, loc = obs.loc)
Y <- as.vector(A %*% x + rnorm(n.obs) * sqrt(sigma2.e))

We now fit the model using rSPDE and inlabru. If we want to obtain an excursion set of the linear predictor evaluated at the mesh, the simplest option is to define a likelihood component in the bru call which contains NA observations at the mesh locations. We then give this component a tag (pred below) so that we can access these later.

rspde_model <- rspde.matern(mesh = mesh, nu = 1.5)
data <- data.frame(x1 = obs.loc[, 1], x2 = obs.loc[, 2], y = Y)
coordinates(data) <- c("x1", "x2")

# data for prediction locations
data.prd <- data.frame(
  x1 = mesh$loc[, 1],
  x2 = mesh$loc[, 2],
  y = rep(NA, dim(mesh$loc)[1])
)
coordinates(data.prd) <- c("x1", "x2")

cmp <- y ~ Intercept(1) + field(coordinates, model = rspde_model)
result_bru <- bru(~ Intercept(1) + field(coordinates, model = rspde_model),
  like(y ~ ., family = "normal", data = data),
  like(y ~ ., family = "normal", data = data.prd, tag = "prd"),
  options = list(
    control.compute = list(return.marginals.predictor = TRUE),
    num.threads = "1:1"
  )
)
#> Warning: `like()` was deprecated in inlabru 2.12.0.
#> ℹ Please use `bru_obs()` instead.
#> This warning is displayed once every 8 hours.
#> Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
#> generated.
#> Warning: The `data` argument of `bru_obs()` has deprecated support for `Spatial` input
#> as of inlabru 2.12.0.9023.
#> ℹ Please use `sf` input instead.
#> ℹ The deprecated feature was likely used in the inlabru package.
#>   Please report the issue at <https://github.com/inlabru-org/inlabru/issues>.
#> This warning is displayed once every 8 hours.
#> Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
#> generated.

We can now compute excursion sets using the excursions.inla function. As no stack object is constructed when using inlabru, we use the argument name = "APredictor" to tell the function that we are interested in the linear predictor. We then use the bru_index function to obtain the indices for the relevant part of the predictor. In this case, we want the indices which correspond to the likelihood component which we gave the tag "pred" above, so the call looks as follows.

res.qc_bru <- excursions.inla(result_bru,
  name = "APredictor",
  ind = bru_index(result_bru, "prd"),
  alpha = 0.99, u = 0,
  method = "QC", type = ">",
  prune.ind = TRUE,
  max.threads = 2
)

Note that we here set prune.ind = TRUE which tells the function that we want the result object only evaluated at the indices specified by the ind argument. We can now obtain a continuous domain representation through the continuous function

sets <- continuous(res.qc_bru, mesh, alpha = 0.1)

Finally, we can plot the results

cmap.F <- colorRampPalette(brewer.pal(9, "Greens"))(100)
proj <- fm_evaluator(sets$F.geometry, dims = c(300, 200))
image(proj$x, proj$y, fm_evaluate(proj, field = sets$F),
  col = cmap.F, axes = FALSE, xlab = "", ylab = "", asp = 1,
  main = "excursion function"
)

comparison of the different types of approximations

Above we used the QC method to compute the set. Let us now try the other available options and compare their timings and results.

t.EB <- system.time(
  res.EB <- excursions.inla(result_bru,
    name = "APredictor",
    ind = bru_index(result_bru, "prd"),
    alpha = 0.99, u = 0,
    method = "EB", type = ">",
    prune.ind = TRUE,
    max.threads = 2
  )
)
t.QC <- system.time(
  res.QC <- excursions.inla(result_bru,
    name = "APredictor",
    ind = bru_index(result_bru, "prd"),
    alpha = 0.99, u = 0,
    method = "QC", type = ">",
    prune.ind = TRUE,
    max.threads = 2
  )
)
t.NI <- system.time(
  res.NI <- excursions.inla(result_bru,
    name = "APredictor",
    ind = bru_index(result_bru, "prd"),
    alpha = 0.99, u = 0,
    method = "NI", type = ">",
    prune.ind = TRUE,
    max.threads = 2
  )
)
t.NIQC <- system.time(
  res.NIQC <- excursions.inla(result_bru,
    name = "APredictor",
    ind = bru_index(result_bru, "prd"),
    alpha = 0.99, u = 0,
    method = "NIQC", type = ">",
    prune.ind = TRUE,
    max.threads = 2
  )
)

The computation time for the different methods are

print(data.frame(
  time = c(t.EB[3], t.QC[3], t.NI[3], t.NIQC[3]),
  row.names = c("EB", "QC", "NI", "NIQC")
))
#>        time
#> EB    3.843
#> QC    4.000
#> NI   37.581
#> NIQC 41.952

We can see that the EB and QC methods have similar computation times and that NI and NIQC take longer. Let us now plot the corresponding sets, we start with the EB result:

image(proj$x, proj$y, fm_evaluate(proj,
  field = continuous(res.EB,
    mesh,
    alpha = 0.1
  )$F
),
col = cmap.F, axes = FALSE, xlab = "", ylab = "", asp = 1,
main = "EB"
)

Then the QC result:

image(proj$x, proj$y, fm_evaluate(proj,
  field = continuous(res.QC,
    mesh,
    alpha = 0.1
  )$F
),
col = cmap.F, axes = FALSE, xlab = "", ylab = "", asp = 1,
main = "QC"
)

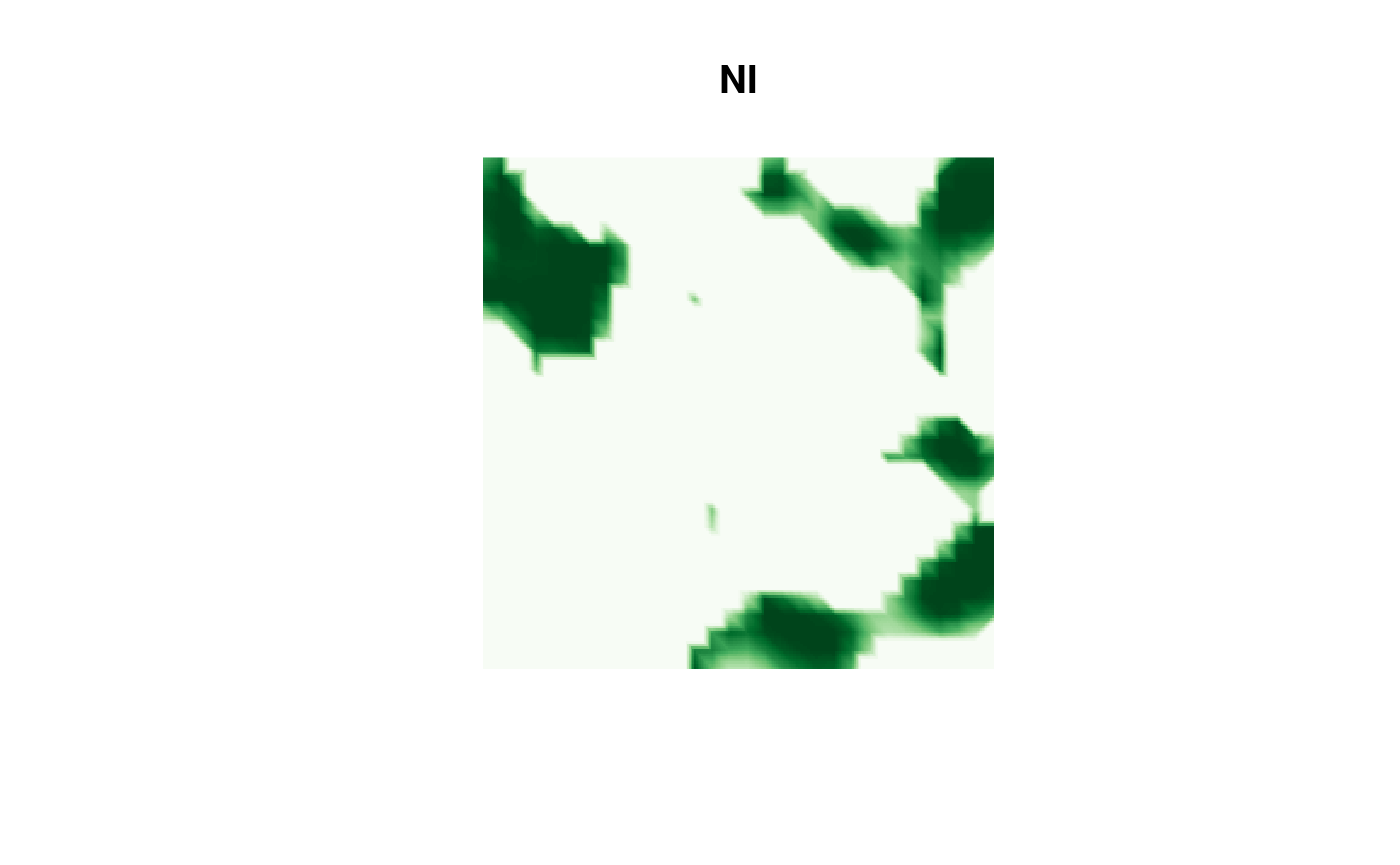
Then the NI result:

image(proj$x, proj$y, fm_evaluate(proj,
  field = continuous(res.NI,
    mesh,
    alpha = 0.1
  )$F
),
col = cmap.F, axes = FALSE, xlab = "", ylab = "", asp = 1,
main = "NI"
)

and finally the NIQC result:

image(proj$x, proj$y, fm_evaluate(proj,
  field = continuous(res.NIQC,
    mesh,
    alpha = 0.1
  )$F
),
col = cmap.F, axes = FALSE, xlab = "", ylab = "", asp = 1,
main = "NIQC"
)

David Bolin and Finn Lindgren

Introduction

comparison of the different types of approximations