Skip to contents

Using excursions with INLA

David Bolin and Finn Lindgren

Source: vignettes/articles/inla.Rmd
inla.Rmd

Introduction

The function excursions.inla is used to compute excursion sets and credible regions for contour curves for latent Gaussian models that have been estimated using INLA. It takes the same arguments excursions, except that mu and Q are replaced with arguments related to INLA. A basic call to the function excursions.inla looks like

excursions.inla(result.inla, name, alpha, u, type)

Here result.inla is the output from a call to the inla function, and name is the name of the component in the output that the computations should be done for. For more complicated models, one typically specifies the model in INLA using an inla.stack object. If this is done, the call to excursions.inla will instead look like

excursions.inla(result.inla, stack, tag, alpha, u, type)

Here stack is now the stack object and tag is the name of the component in the stack for which the computations should be done. The typical usage of the tag argument is to have one part of the stack that contains the locations where measurements are taken, and another that contains the locations where the output should be computed.

excursions.inla has support for all strategies described in Definitions and computational methodology for handling latent Gaussian structures: The argument method can be one of 'EB', 'QC', 'NI', 'NIQC', and 'iNIQC'.

Similarly contourmap.inla and simconf.inla are the INLA versions of the contourmap and simconf functions. The model specification using these functions is identical to that in the excursions.inla function. We now provide two applications to illustrate the methods of the package using the INLA interface.

An example using a simultaneous confidence bands

We start by a temporal example to illustrate how a simultaneous confidence band can be created using simconf.inla. We use the much analyzed binomial time series from (Kitagawa 1987). Each day during the years 1983 and 1984, it was recorded whether there was more than 1 mm rainfall in Tokyo. Of interest is to study the underlying probability of rainfall as a function of day of the year. The data is modelled as yi∼Bin(ni,pi)y_i \sim Bin(n_i,p_i) for calendar day i=1,…,366i = 1,\dots,366. Here ni=2n_i = 2 for all days except for February 29 (i=60i=60) which only occurred during the leap year of 1984. The probability pip_i is modeled as a logit-transformed Gaussian process.

The model and the following INLA implementation of the model is described further in (Lindgren and Rue 2015).

data("Tokyo")
mesh <- fm_mesh_1d(seq(1, 367, length = 25),
  interval = c(1, 367),
  degree = 2, boundary = "cyclic"
)
kappa <- 1e-3
tau <- 1 / (4 * kappa^3)^0.5
spde <- inla.spde2.matern(mesh,
  constr = FALSE,
  theta.prior.prec = 1e-4,
  B.tau = cbind(log(tau), 1),
  B.kappa = cbind(log(kappa), 0)
)
A <- inla.spde.make.A(mesh, loc = Tokyo$time)
time.index <- inla.spde.make.index("time", n.spde = spde$n.spde)
stack <- inla.stack(
  data = list(y = Tokyo$y, link = 1, Ntrials = Tokyo$n),
  A = list(A), effects = list(time.index), tag = "est"
)
data <- inla.stack.data(stack)

Next, the model is estimated using the inla function. Since we want to analyze the output using excursions, the additional option control.compute = list(config = TRUE) must be specified in the inla function. This makes the function save some extra output needed by excursions.

result <- inla(y ~ -1 + f(time, model = spde),
  family = "binomial",
  data = data,
  Ntrials = data$Ntrials,
  control.predictor = list(
    A = inla.stack.A(stack),
    link = data$link,
    compute = TRUE
  ),
  control.compute = list(config = TRUE),
  num.threads = "1:1"
)

We now have estimates of the posterior mean and marginal confidence intervals for the probability of rain for each day. However, if we also want joint confidence bands, we can estimate these using simconf.inla as

res <- simconf.inla(result, stack,
  tag = "est", alpha = 0.05, link = TRUE,
  max.threads = 2
)

Note the argument link=TRUE which tells the function that the results should be returned in the scale of the data, and not in the scale of the linear predictor. Next, we plot the results, showing the marginal confidence bands with dashed lines and the simultaneous confidence band with dotted lines.

index <- inla.stack.index(stack, "est")$data
plot(Tokyo$time, Tokyo$y / Tokyo$n, xlab = "Day", ylab = "Probability", pch = 20)
lines(result$summary.fitted.values$mean[index])
matplot(cbind(res$a.marginal, res$b.marginal),
  type = "l", lty = 2,
  col = 1, add = TRUE
)
matplot(cbind(res$a, res$b), type = "l", lty = 3, col = 2, add = TRUE)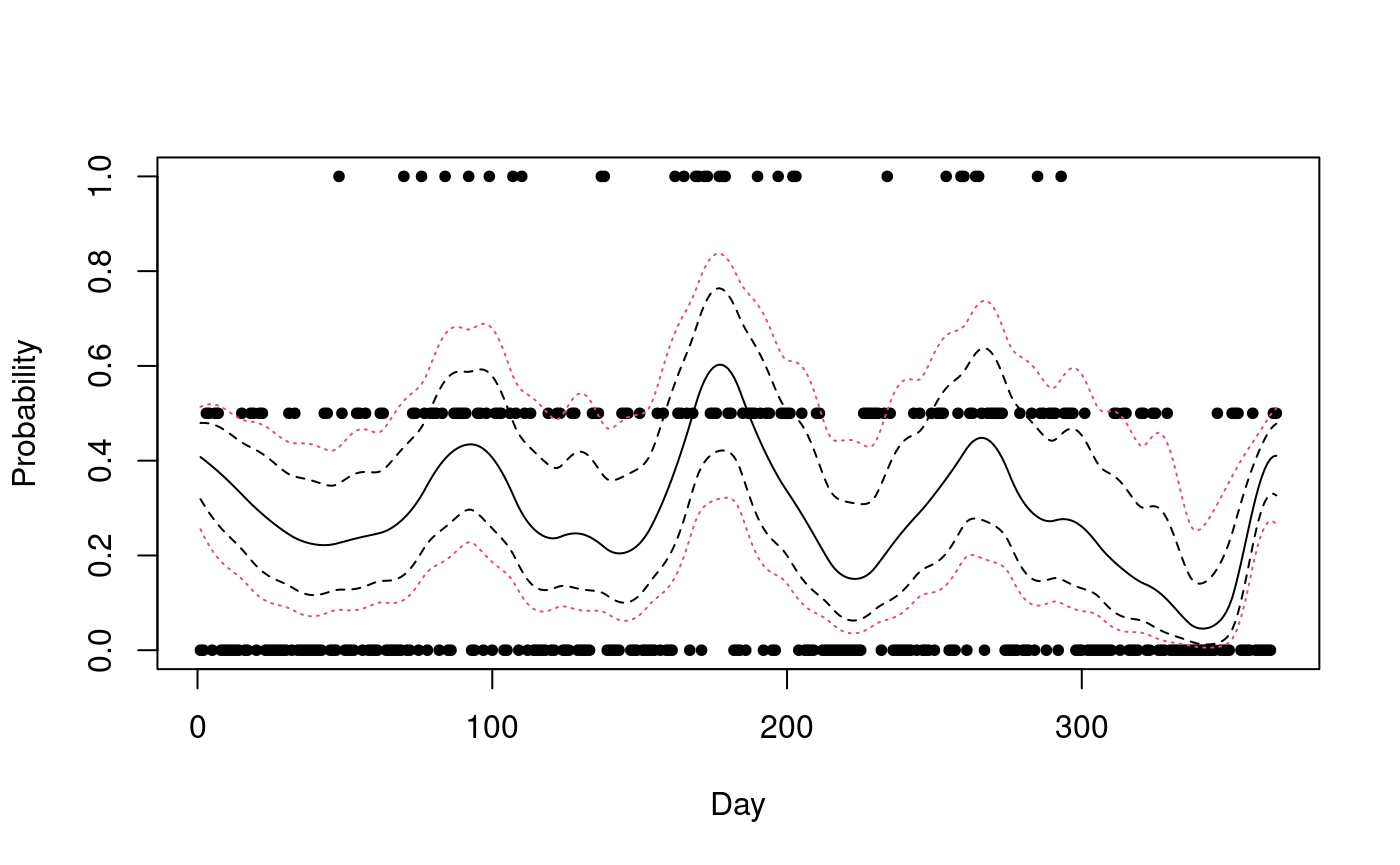

A spatial example

We will now use a spatial dataset to illustrate how excursions can be used. In order to keep the parts of the code that are not relevant to excursions brief, we again use data available in INLA. The dataset consists of daily rainfall data for each day of the year 2011, at 616 locations in and around the stated of Paran'a in Brazil. In the following analysis, we analyze the data from the month of January.

The statistical model used for the data is a latent Gaussian model, where the precipitation measurements are assumed to be Γ\Gamma-distributed with a spatially varying mean. The mean is modeled as a log-Gaussian Mat'ern field specified as an SPDE model. Details of the current model model and the following INLA implementation can be found in the SPDE tutorial available on the INLA homepage, see (Wallin and Bolin 2015) for an analysis of the data using a different non-Gaussian SPDE model.

We start by loading the data and defining the model:

data("PRprec")
data("PRborder")
Y <- rowMeans(PRprec[, 3 + (1:31)])
ind <- !is.na(Y)
Y <- Y[ind]
coords <- as.matrix(PRprec[ind, 1:2])
b <- fm_nonconvex_hull(coords, -0.03, -0.05, resolution = c(100, 100))
prmesh <- fm_mesh_2d(boundary = b, max.edge = c(.45, 1), cutoff = 0.2)
A <- inla.spde.make.A(prmesh, loc = coords)
spde <- inla.spde2.matern(prmesh, alpha = 2)
mesh.index <- inla.spde.make.index(name = "field", n.spde = spde$n.spde)

The measurement stations are spatially irregular, but we are interested in making predictions to a regular lattice within the state. In order to do continuous domain interpretations, we define the lattice locations as a lattice object using the submesh function of the excursions package. The function inout from the package splancs is used to find the locations on the lattice that are within the region of interest.

nxy <- c(50, 50)
projgrid <- fm_evaluator(
  prmesh,
  xlim = range(PRborder[, 1]),
  ylim = range(PRborder[, 2]),
  dims = nxy
)
xy.in <- inout(projgrid$lattice$loc, cbind(PRborder[, 1], PRborder[, 2]))
submesh <- submesh.grid(
  matrix(xy.in, nxy[1], nxy[2]),
  list(loc = projgrid$lattice$loc, dims = nxy)
)

We now define the stack objects and estimate the model using inla. Again note that we have to set the control.compute argument of the results is to be used by excursions.

A.prd <- inla.spde.make.A(prmesh, loc = submesh$loc)
stk.prd <- inla.stack(
  data = list(y = NA), A = list(A.prd, 1),
  effects = list(
    c(mesh.index, list(Intercept = 1)),
    list(
      lat = submesh$loc[, 2],
      lon = submesh$loc[, 1]
    )
  ),
  tag = "prd"
)
stk.dat <- inla.stack(
  data = list(y = Y), A = list(A, 1),
  effects = list(
    c(mesh.index, list(Intercept = 1)),
    list(
      lat = coords[, 2],
      lon = coords[, 1]
    )
  ),
  tag = "est"
)
stk <- inla.stack(stk.dat, stk.prd)
r <- inla(y ~ -1 + Intercept + f(field, model = spde),
  family = "Gamma",
  data = inla.stack.data(stk),
  control.compute = list(
    config = TRUE,
    return.marginals.predictor = TRUE
  ),
  control.predictor = list(
    A = inla.stack.A(stk),
    compute = TRUE,
    link = 1
  ),
  num.threads = "1:1"
)

We now want to find areas that likely experienced large amounts of precipitation. In the following code, we compute the excursion set for the posterior mean for the level 77 mm of precipitation. To indicate that this level is in the scale of the data, and not in the scale of the linear predictor, we use the u.link=TRUE argument in the excursions call.

exc <- excursions.inla(r, stk,
  tag = "prd", u = 7, u.link = TRUE,
  type = ">", F.limit = 0.6, method = "QC",
  max.threads = 2
)
sets <- continuous(exc, submesh, alpha = 0.1)

We also compute the contour curve for the level of interest on the continuous domain, using the tricontourmap function.

con <- tricontourmap(submesh, z = exc$mean, levels = log(7))

We plot the resulting continuous domain excursion function together with the contour curve using the following commands.

cmap.F <- colorRampPalette(brewer.pal(9, "Greens"))(100)
proj <- fm_evaluator(sets$F.geometry, dims = c(300, 200))
image(proj$x, proj$y, fm_evaluate(proj, field = sets$F),
  col = cmap.F, axes = FALSE, xlab = "", ylab = "", asp = 1
)
plot(con$map, add = TRUE)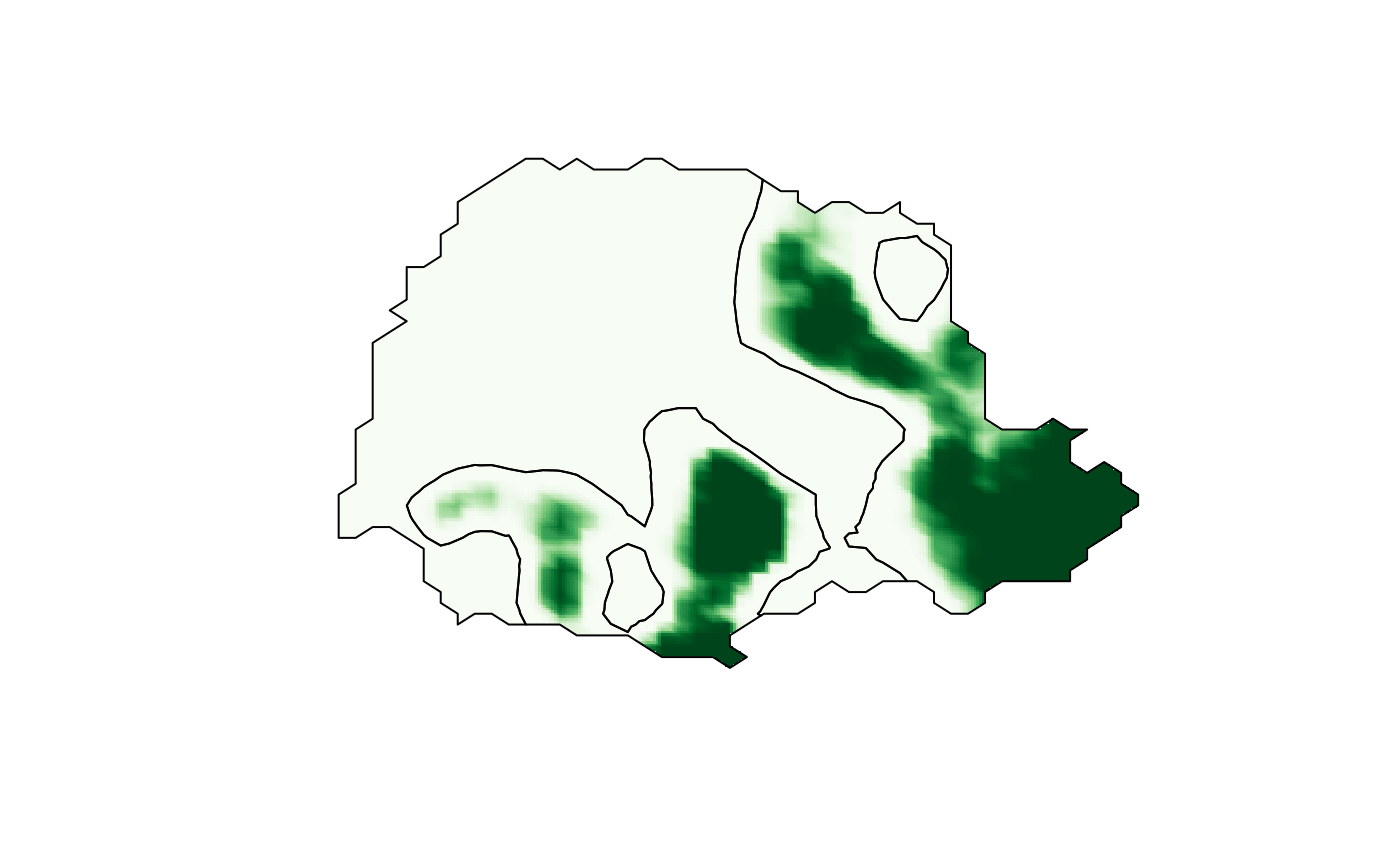

To visualize the posterior mean using a contour map using the following commands

cmap <- colorRampPalette(brewer.pal(9, "YlGnBu"))(100)
lp <- contourmap.inla(r,
  stack = stk, tag = "prd", n.levels = 2,
  compute = list(F = FALSE)
)
tmap <- tricontourmap(submesh, z = lp$meta$mu, levels = lp$meta$levels)
plot(tmap$map, col = contourmap.colors(lp, col = cmap))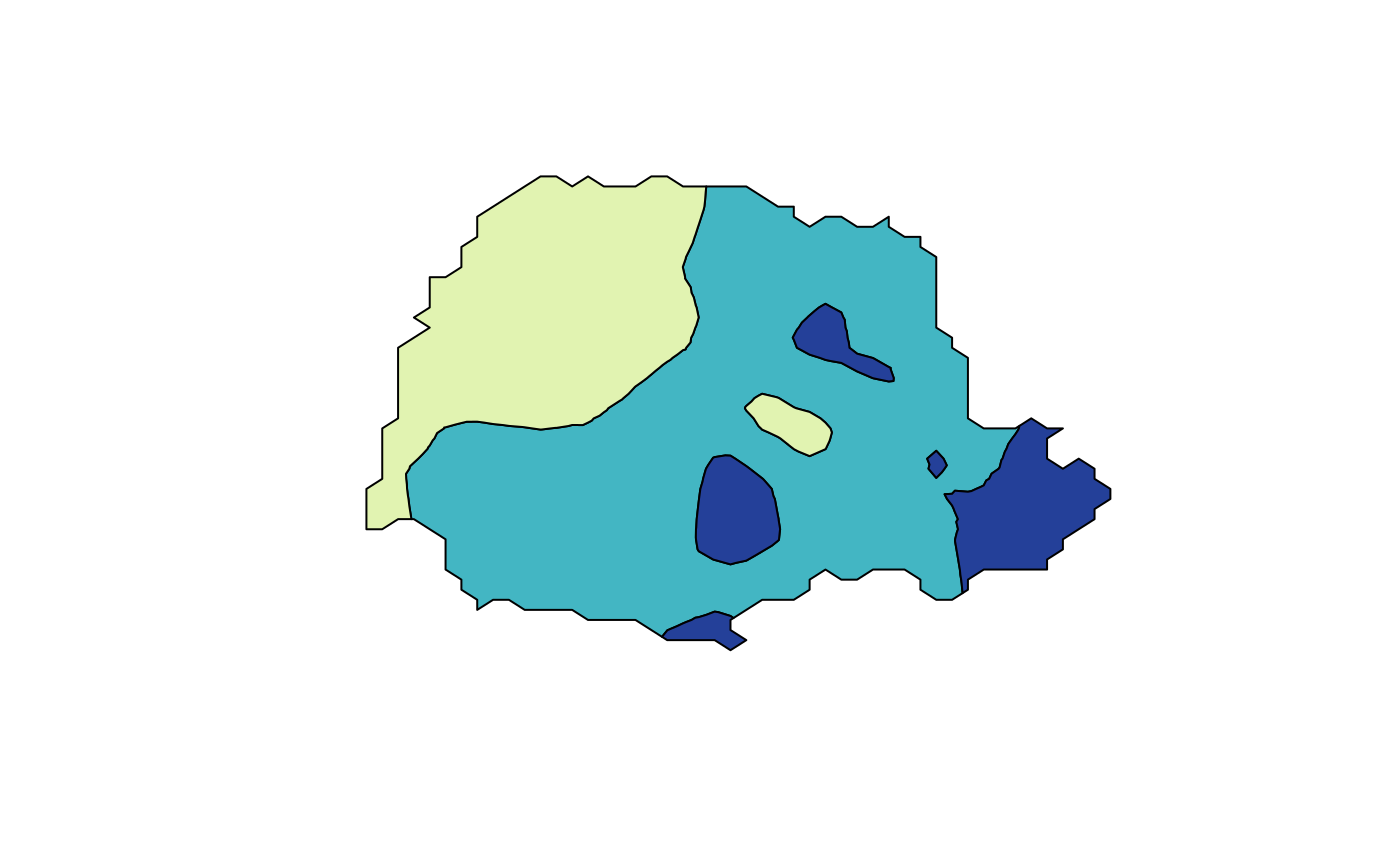

Here, the contourmap.inla computes the levels of the contour map and tricontourmap computes the contour map on the mesh. Finally, contourmap.colors is used to compute appropriate colours for visualizing the contour map.

The contour map we computed had two contours, and a relevant question is now if this is an appropriate number. To investigate this, we compute the P2P_2 quality measure for this contour map and for contour maps with one and three levels.

lps <- list()
for (i in 1:4) {
  lps[[i]] <- contourmap.inla(r,
    stack = stk, tag = "prd", n.levels = i,
    compute = list(F = FALSE, measures = c("P2")),
    max.threads = 2
  )
}
print(data.frame(
  P2 = c(lps[[1]]$P2, lps[[2]]$P2, lps[[3]]$P2, lps[[4]]$P2),
  row.names = c(
    "n.level = 1", "n.level = 2",
    "n.level = 3", "n.level = 4"
  )
))
#>                       P2
#> n.level = 1 0.9999999965
#> n.level = 2 0.6536138326
#> n.level = 3 0.0337021714
#> n.level = 4 0.0001892985

We see that using only one or two contours give very high credibility, whereas using four contours give a credibility that is close to zero. The contour map with three contours has a credibility around 0.20.2 and seems to be a good compromise for this application.

References

Kitagawa, Genshiro. 1987. “Non-Gaussian State-Space Modeling of Nonstationary Time Series.” Journal of the American Statistical Association 82 (400): 1032–41. https://doi.org/10.1080/01621459.1987.10478534.
Lindgren, F., and H. Rue. 2015. “Bayesian Spatial and Spatiotemporal Modelling with .” Journal of Statistical Software 63 (19). https://doi.org/10.18637/jss.v063.i19.
Wallin, Jonas, and David Bolin. 2015. “Geostatistical Modelling Using Non-Gaussian Matérn Fields.” Scandinavian Journal of Statistics 42: 872–90. https://doi.org/10.1111/sjos.12141.