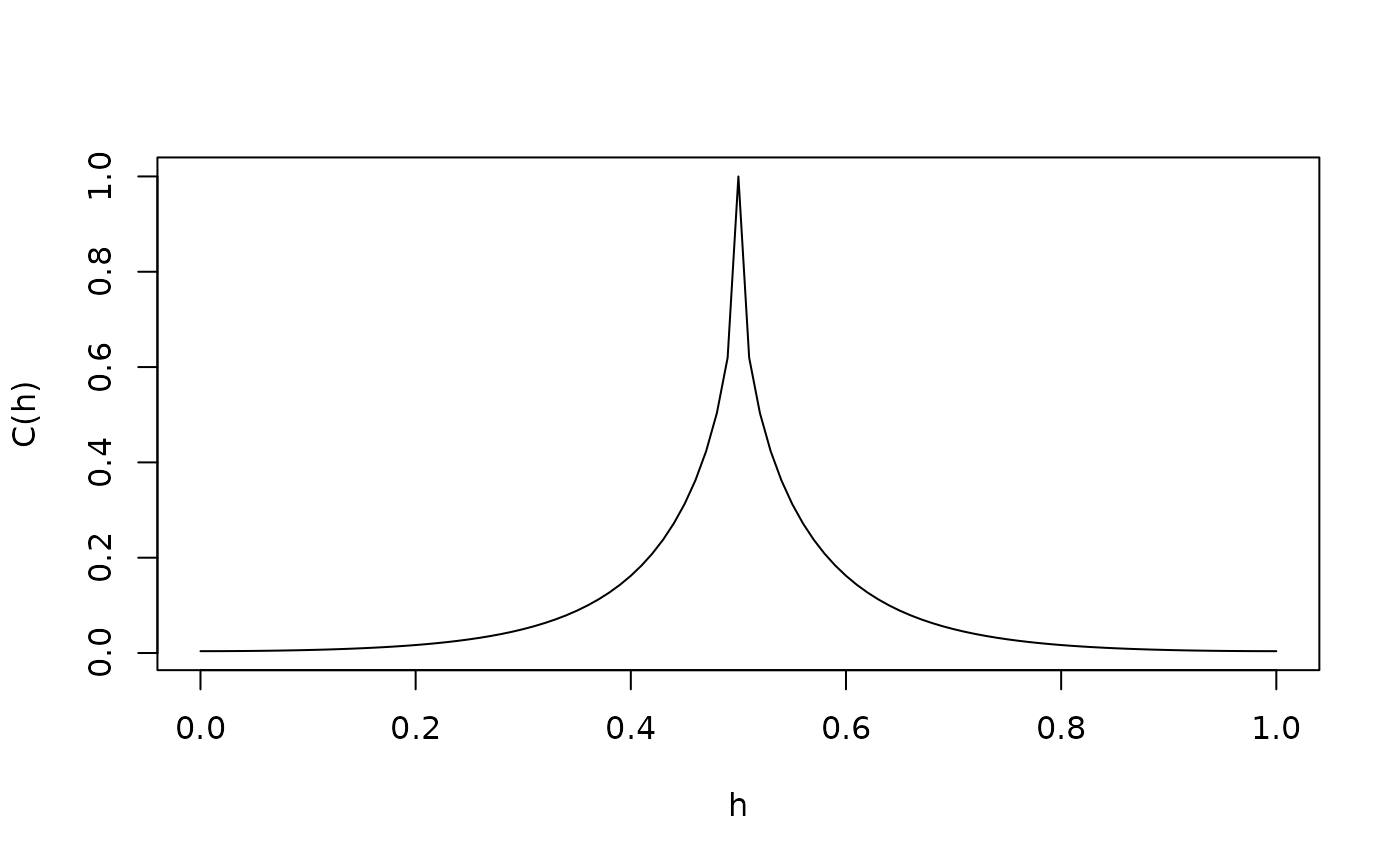
The 1d folded Matern covariance function

folded.matern.covariance.1d evaluates the 1d folded Matern covariance function over an interval \([0,L]\).

Usage

folded.matern.covariance.1d(
  h,
  m,
  kappa,
  nu,
  sigma,
  L = 1,
  N = 10,
  boundary = c("neumann", "dirichlet", "periodic")
)

Arguments

h, m

Vectors of arguments of the covariance function.

kappa

Range parameter.

nu

Shape parameter.

sigma

Standard deviation.

L

The upper bound of the interval \([0,L]\). By default, L=1.

N

The truncation parameter.

boundary

The boundary condition. The possible conditions are "neumann" (default), "dirichlet" or "periodic".

Value

A matrix with the corresponding covariance values.

Details

folded.matern.covariance.1d evaluates the 1d folded Matern covariance function over an interval \([0,L]\) under different boundary conditions. For periodic boundary conditions $$C_{\mathcal{P}}(h,m) = \sum_{k=-\infty}^{\infty} (C(h-m+2kL),$$ for Neumann boundary conditions $$C_{\mathcal{N}}(h,m) = \sum_{k=-\infty}^{\infty} (C(h-m+2kL)+C(h+m+2kL)),$$ and for Dirichlet boundary conditions: $$C_{\mathcal{D}}(h,m) = \sum_{k=-\infty}^{\infty} (C(h-m+2kL)-C(h+m+2kL)),$$ where \(C(\cdot)\) is the Matern covariance function: $$C(h) = \frac{\sigma^2}{2^{\nu-1}\Gamma(\nu)}(\kappa h)^\nu K_\nu(\kappa h).$$

We consider the truncation: $$C_{{\mathcal{P}},N}(h,m) = \sum_{k=-N}^{N} C(h-m+2kL), C_{\mathcal{N},N}(h,m) = \sum_{k=-\infty}^{\infty} (C(h-m+2kL)+C(h+m+2kL)),$$ and $$C_{\mathcal{D},N}(h,m) = \sum_{k=-N}^{N} (C(h-m+2kL)-C(h+m+2kL)).$$

Examples

x <- seq(from = 0, to = 1, length.out = 101)
plot(x, folded.matern.covariance.1d(rep(0.5, length(x)), x,
  kappa = 10, nu = 1 / 5, sigma = 1
),
type = "l", ylab = "C(h)", xlab = "h"
)