Skip to contents

Anisotropic models

David Bolin and Alexandre B. Simas

Created: 2024-10-23. Last modified: 2024-12-20.

Source: vignettes/anisotropic.Rmd
anisotropic.Rmd

Introduction

For domains D⊂ℝ2D\subset \mathbb{R}^2, the rSPDE package implements the anisotropic Matérn model (I−∇⋅(H∇))(ν+1)/2u=cσW,on D (I - \nabla\cdot (H\nabla))^{(\nu + 1)/2} u = c\sigma W, \quad \text{on } D Where HH is a 2×22\times 2 positive definite matrix, σ,ν>0\sigma, \nu >0 and cc is a constant chosen such that uu would have the covariance function r(h)=σ22ν−1Γ(ν)(hTH−1h)νKν(hTH−1h), r(h) = \frac{\sigma^2}{2^{\nu-1}\Gamma(\nu)} (\sqrt{h^T H^{-1} h})^{\nu} K_{\nu}(\sqrt{h^T H^{-1} h}), if the domain was D=ℝ2D = \mathbb{R}^2, i.e., a stationary and anisotropic Matérn covariance function. The matrix HH is defined as H=[hx2hxhyhxyhxhyhxyhy2] H = \begin{bmatrix} h_x^2 & h_xh_y h_{xy}\\ h_xh_y h_{xy} & h_y^2 \end{bmatrix} with hx,hy>0h_x,h_y>0 and hxy∈(−1,1)h_{xy} \in (-1,1).

Implementation details

Let us begin by loading some packages needed for making the plots

We start by creating a region of interest and a spatial mesh using the fmesher package:

library(fmesher)
n_loc <- 2000
loc_2d_mesh <- matrix(runif(n_loc * 2), n_loc, 2)
mesh_2d <- fm_mesh_2d(
    loc = loc_2d_mesh,
    cutoff = 0.01,
    max.edge = c(0.1, 0.5)
)
plot(mesh_2d, main = "")

We now specify the model using the matern2d.operators function.

sigma <- 1
nu = 0.5
hx <- 0.08
hy <- 0.08
hxy <- 0.5
op <- matern2d.operators(hx = hx, hy = hy, hxy = hxy, nu = nu, 
                         sigma = sigma, mesh = mesh_2d)

The matern2d.operators object has cov_function_mesh method which can be used evaluate the covariance function on the mesh. For example

r <- op$cov_function_mesh(matrix(c(0.5,0.5),1,2))
proj <- fm_evaluator(mesh_2d, dims = c(100, 100), xlim = c(0,1), ylim = c(0,1))
r.mesh <- fm_evaluate(proj, field = as.vector(r))
cov.df <- data.frame(x1 = proj$lattice$loc[,1],
                     x2 = proj$lattice$loc[,2], 
                     cov = c(r.mesh))
ggplot(cov.df, aes(x = x1, y = x2, fill = cov)) + geom_raster() + xlim(0,1) + ylim(0,1) + scale_fill_viridis()
#> Warning: Removed 396 rows containing missing values or values outside the scale range
#> (`geom_raster()`).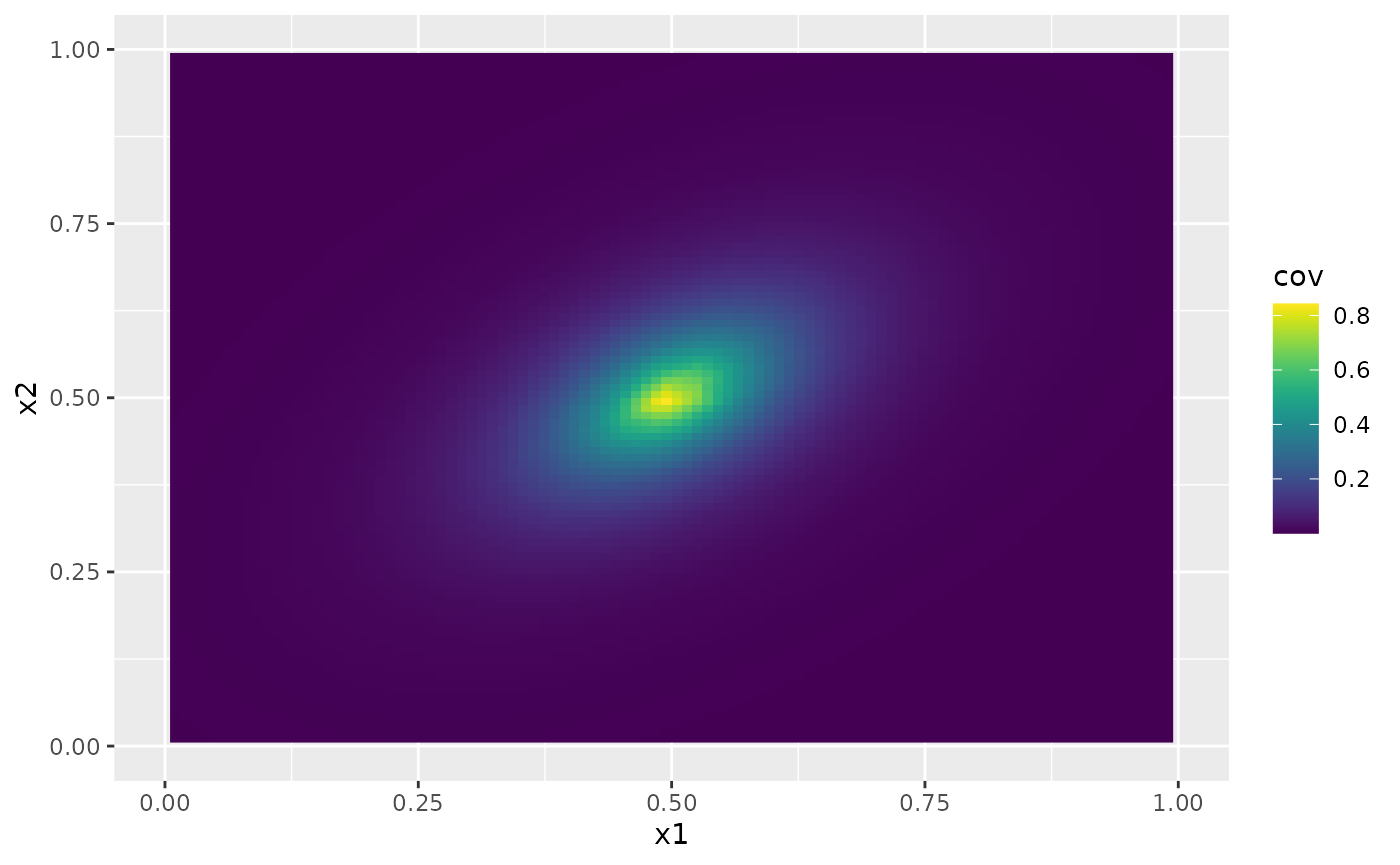

We can simulate from the field using the simulate method:

u <- simulate(op)
proj <- fm_evaluator(mesh_2d, dims = c(100, 100), xlim = c(0,1), ylim = c(0,1))
u.mesh <- fm_evaluate(proj, field = as.vector(u))
cov.df <- data.frame(x1 = proj$lattice$loc[,1],
                     x2 = proj$lattice$loc[,2], 
                     u = c(u.mesh))
ggplot(cov.df, aes(x = x1, y = x2, fill = u)) + geom_raster() + xlim(0,1) + ylim(0,1) + scale_fill_viridis()
#> Warning: Removed 396 rows containing missing values or values outside the scale range
#> (`geom_raster()`).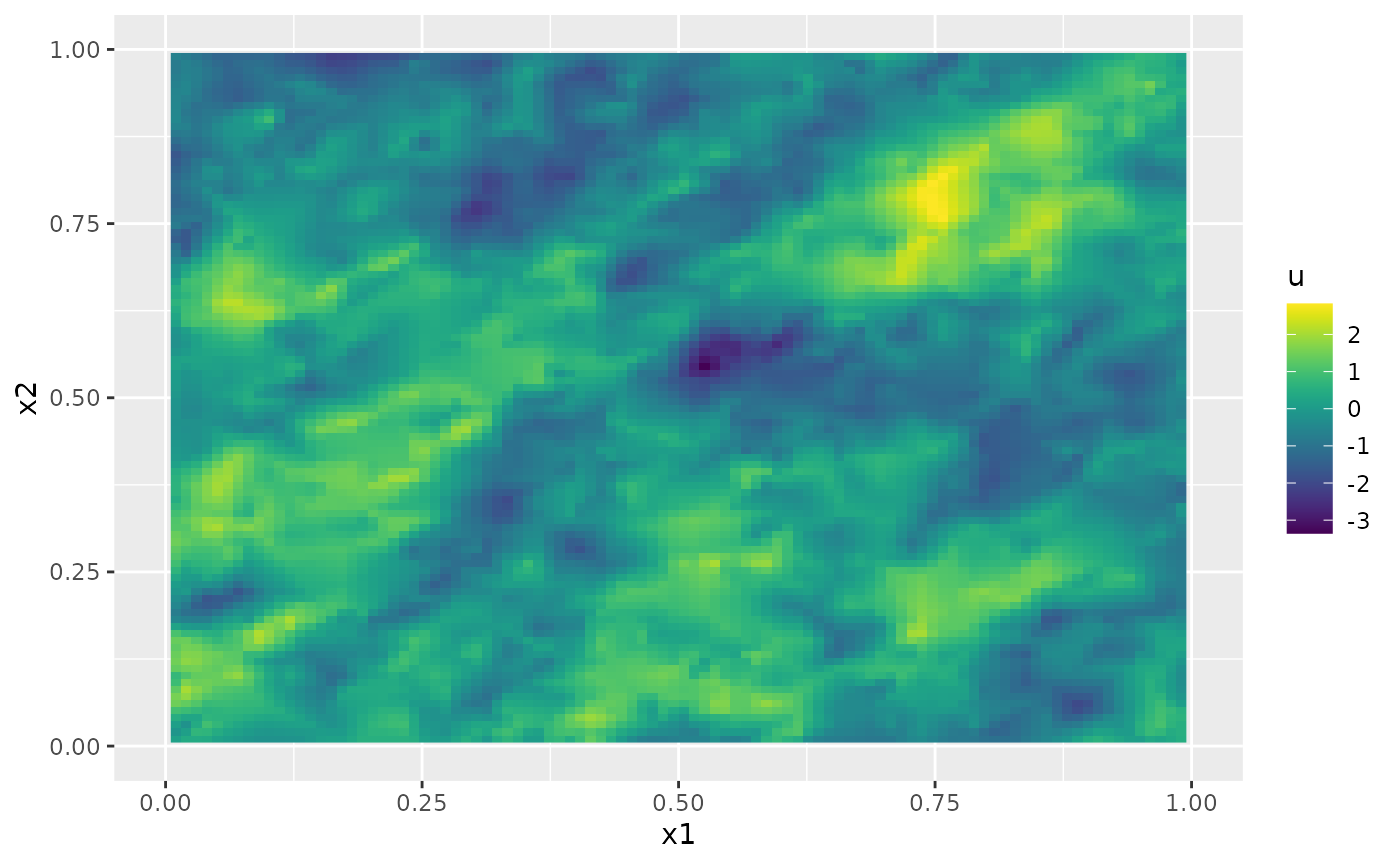

Let us now simulate some data based on this simulated field.

n.obs <- 2000
obs.loc <- cbind(runif(n.obs),runif(n.obs))
A <- fm_basis(mesh_2d,obs.loc)
sigma.e <- 0.1
Y <- as.vector(A%*%u + sigma.e*rnorm(n.obs))

We can compute kriging predictions of the process uu based on these observations. To specify which locations that should be predicted, the argument Aprd is used. This argument should be an observation matrix that links the mesh locations to the prediction locations.

A <- op$make_A(obs.loc)
Aprd <- op$make_A(proj$lattice$loc)
u.krig <- predict(op, A = A, Aprd = Aprd, Y = Y, sigma.e = sigma.e)

The process simulation, and the kriging prediction are shown in the following figure.

data.df <- data.frame(x = obs.loc[,1], y = obs.loc[,2], field = Y, type = "Data")
krig.df <- data.frame(x = proj$lattice$loc[,1], y = proj$lattice$loc[,2],
                      field = as.vector(u.krig$mean), type = "Prediction")
df_plot <- rbind(data.df, krig.df)
ggplot(df_plot) + aes(x = x, y = y, fill = field) +
        facet_wrap(~type) + geom_raster(data = krig.df) +
        geom_point(data = data.df, aes(colour = field),
        show.legend = FALSE) + 
        scale_fill_viridis() + scale_colour_viridis()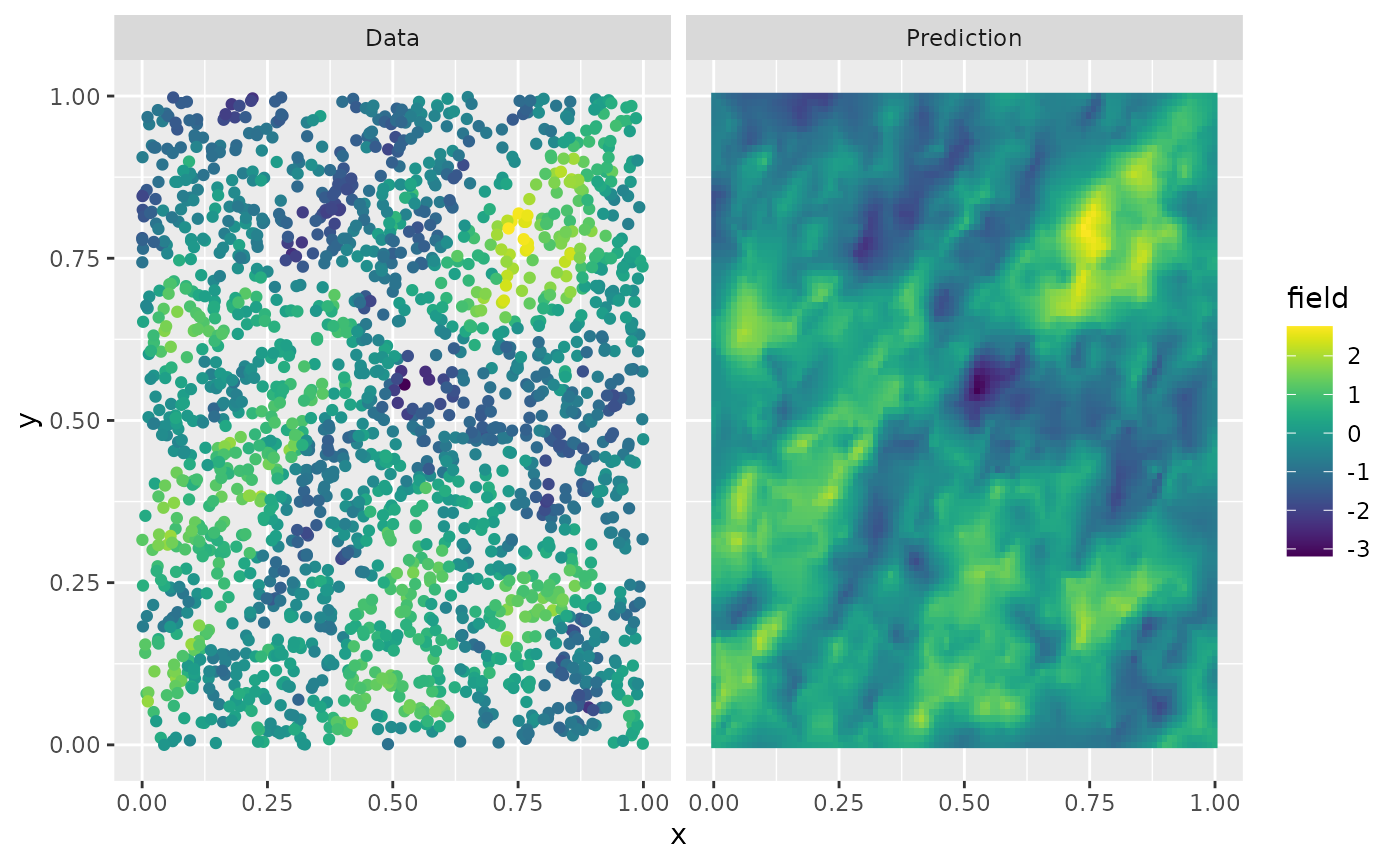

Let us finally use rspde_lme to estimate the parameters based on the data.

df <- data.frame(Y = as.matrix(Y), x = obs.loc[,1], y = obs.loc[,2])
res <- rspde_lme(Y ~ 1, loc = c("x","y"), data = df, model = op, parallel = TRUE)
#> Warning in rspde_lme(Y ~ 1, loc = c("x", "y"), data = df, model = op, parallel
#> = TRUE): The optimization failed to provide a numerically positive-definite
#> Hessian. You can try to obtain a positive-definite Hessian by setting
#> 'improve_hessian' to TRUE or by setting 'parallel' to FALSE, which allows other
#> optimization methods to be used.
#> Warning in sqrt(diag(inv_fisher)): NaNs produced

In the call, y~1 indicates that we also want to estimate a mean value of the model, and the arguments loc provides the names of the spatial and temporal coordinates in the data frame. Let us see a summary of the fitted model:

summary(res)
#> 
#> Latent model - Anisotropic Whittle-Matern
#> 
#> Call:
#> rspde_lme(formula = Y ~ 1, loc = c("x", "y"), data = df, model = op, 
#>     parallel = TRUE)
#> 
#> Fixed effects:
#>             Estimate Std.error z-value Pr(>|z|)
#> (Intercept)  -0.1590    0.1567  -1.015     0.31
#> 
#> Random effects:
#>       Estimate Std.error z-value
#> nu     0.45296       NaN     NaN
#> sigma  0.96753   0.03504  27.616
#> hx     0.09255   0.01727   5.359
#> hy     0.09426   0.01750   5.386
#> hxy    0.55628   0.05128  10.848
#> 
#> Measurement error:
#>          Estimate Std.error z-value
#> std. dev 0.100588  0.002728   36.87
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 
#> 
#> Log-Likelihood:  -88.82101 
#> Number of function calls by 'optim' = 51
#> Optimization method used in 'optim' = L-BFGS-B
#> 
#> Time used to:     fit the model =  28.24577 secs 
#>   set up the parallelization = 4.78492 secs

Let us compare the estimated results with the true values:

results <- data.frame(sigma = c(sigma, res$coeff$random_effects[2]),
                      hx = c(hx, res$coeff$random_effects[3]), 
                      hy = c(hy, res$coeff$random_effects[4]),
                      hxy = c(hxy, res$coeff$random_effects[5]),
                      nu = c(nu, res$coeff$random_effects[1]),
                      sigma.e = c(sigma.e, res$coeff$measurement_error),
                      intercept = c(0, res$coeff$fixed_effects),
                      row.names = c("True", "Estimate"))
                      
print(results)
#>              sigma         hx         hy       hxy        nu   sigma.e
#> True     1.0000000 0.08000000 0.08000000 0.5000000 0.5000000 0.1000000
#> Estimate 0.9675335 0.09254768 0.09426337 0.5562763 0.4529577 0.1005883
#>           intercept
#> True      0.0000000
#> Estimate -0.1590023

Finally, we can also do prediction based on the fitted model as

pred.data <- data.frame(x = proj$lattice$loc[,1], y = proj$lattice$loc[,2])
pred <- predict(res, newdata = pred.data, loc = c("x","y"))

data.df <- data.frame(x = obs.loc[,1], y = obs.loc[,2], field = Y, type = "Data")
krig.df <- data.frame(x = proj$lattice$loc[,1], y = proj$lattice$loc[,2],
                      field = as.vector(u.krig$mean), type = "Prediction")
df_plot <- rbind(data.df, krig.df)
ggplot(df_plot) + aes(x = x, y = y, fill = field) +
        facet_wrap(~type) + geom_raster(data = krig.df) +
        geom_point(data = data.df, aes(colour = field),
        show.legend = FALSE) + 
        scale_fill_viridis() + scale_colour_viridis()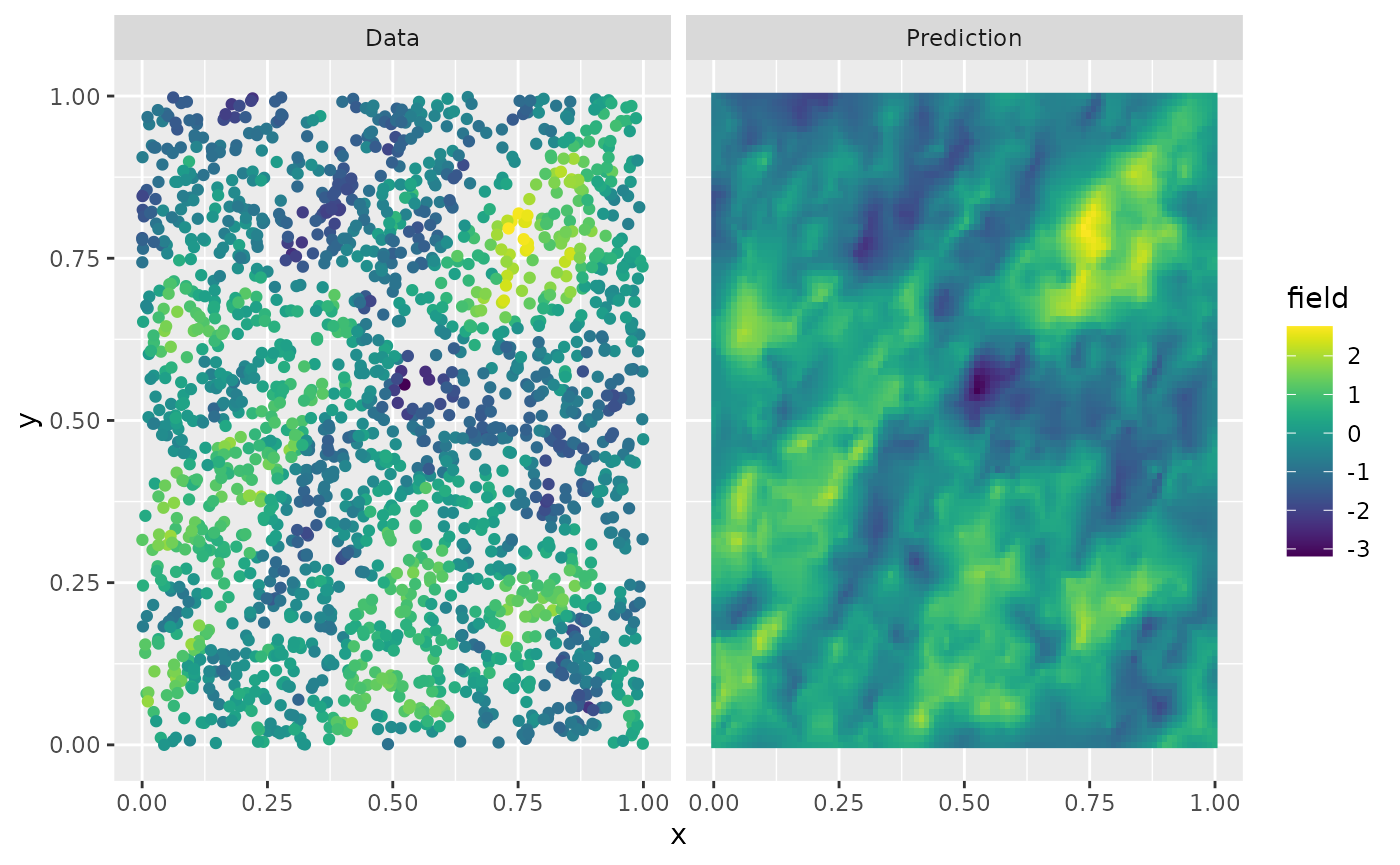

Inlabru Implementation

We will now fit the model using the inlabru package. First, we load the package, and create the anisotropic model object:

library(inlabru)

model_aniso <- rspde.anistropic2d(mesh = mesh_2d)

Then we create the component and fit the model using the inlabru package. Observe that we can use the same data frame as in the rspde_lme example.

cmp <- Y ~ Intercept(1) - 1 + field(cbind(x,y), model = model_aniso)
bru_fit_field <- bru(cmp, data = df, options = list(num.threads = "1:1"))

Let us now compare the estimated results (the means of the parameters) with the true values. Observe that we are using the helper function transform_parameters_anisotropic() to change the scale of the estimated parameters back to the original scale.

results <- data.frame(
  rbind(
    # True values
    c(hx = hx, hy = hy, hxy = hxy, sigma = sigma, nu = nu),
    # Estimated values transformed using transform_parameters_anisotropic
    transform_parameters_anisotropic(
      bru_fit_field$summary.hyperpar$mean[2:6],
      model_aniso[["nu_upper_bound"]]
    )
  ),
  # Add sigma.e values
  sigma.e = c(sigma.e, sqrt(1 / bru_fit_field$summary.hyperpar$mean[1])),
  # Add intercept values
  intercept = c(0, bru_fit_field$summary.fixed$mean),
  row.names = c("True", "Estimate")
)

print(results)
#>                  hx         hy       hxy     sigma        nu   sigma.e
#> True           0.08       0.08       0.5         1       0.5 0.1000000
#> Estimate 0.09779554 0.09940151 0.5555206 0.9850088 0.4663209 0.1004149
#>           intercept
#> True      0.0000000
#> Estimate -0.1698077