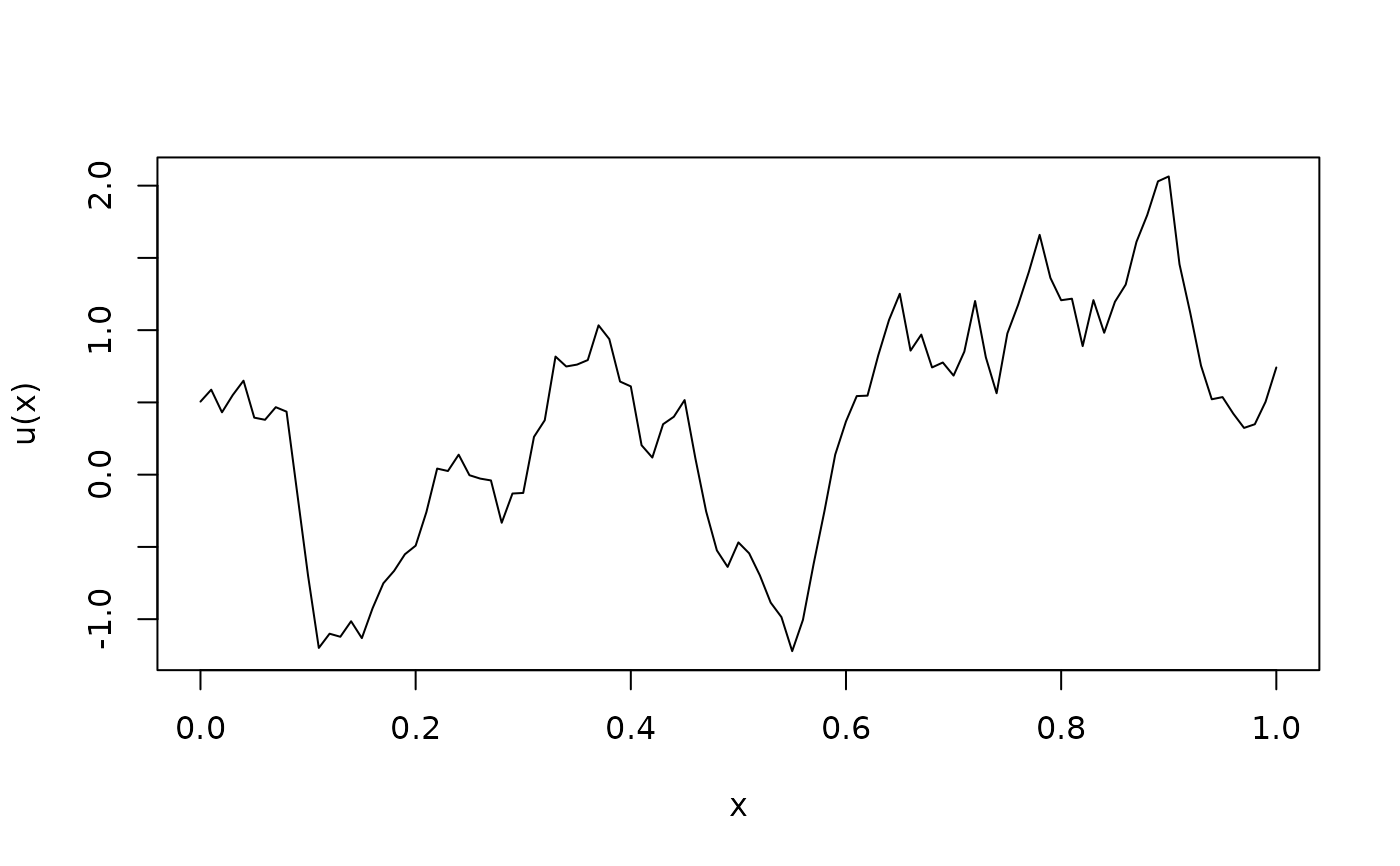
Simulation of a fractional SPDE using the covariance-based rational SPDE approximation

The function samples a Gaussian random field based using the covariance-based rational SPDE approximation.

Usage

# S3 method for class 'CBrSPDEobj'
simulate(
  object,
  nsim = 1,
  seed = NULL,
  nu = NULL,
  kappa = NULL,
  sigma = NULL,
  range = NULL,
  tau = NULL,
  theta = NULL,
  m = NULL,
  ...
)

Arguments

object: The covariance-based rational SPDE approximation, computed using matern.operators()
nsim: The number of simulations.
seed: An object specifying if and how the random number generator should be initialized (‘seeded’).
nu: If non-null, update the shape parameter of the covariance function.
kappa: If non-null, update the range parameter of the covariance function.
sigma: If non-null, update the standard deviation of the covariance function.
range: If non-null, update the range parameter of the covariance function.
tau: If non-null, update the parameter tau.
theta: For non-stationary models. If non-null, update the vector of parameters.
m: If non-null, update the order of the rational approximation, which needs to be a positive integer.
...: Currently not used.

Value

A matrix with the n samples as columns.

Examples

# Sample a Gaussian Matern process on R using a rational approximation
kappa <- 10
sigma <- 1
nu <- 0.8
range <- sqrt(8 * nu) / kappa

# create mass and stiffness matrices for a FEM discretization
x <- seq(from = 0, to = 1, length.out = 101)
fem <- rSPDE.fem1d(x)

# compute rational approximation of covariance function at 0.5
tau <- sqrt(gamma(nu) / (sigma^2 * kappa^(2 * nu) *
  (4 * pi)^(1 / 2) * gamma(nu + 1 / 2)))
op_cov <- matern.operators(
  loc_mesh = x, nu = nu,
  range = range, sigma = sigma, d = 1, m = 2,
  parameterization = "matern"
)

# Sample the model and plot the result
Y <- simulate(op_cov)
plot(x, Y, type = "l", ylab = "u(x)", xlab = "x")