The Inverse-Gaussian (IG) Distribution

Density, distribution function, quantile function and random generation for the inverse-Gaussian distribution with parameters a and b.

dig(x, a, b, log = FALSE)

rig(n, a, b, seed = 0)

pig(q, a, b, lower.tail = TRUE, log.p = FALSE)

qig(p, a, b, lower.tail = TRUE, log.p = FALSE)

Arguments

x, q: vector of quantiles.
a, b: parameters a and b. Must be positive.
log, log.p: logical; if TRUE, probabilities/densities $p$ are returned as $log(p)$.
n,: number of observations.
seed: Seed for the random generation.
lower.tail: logical; if TRUE, probabilities are $P[X\leq x]$, otherwise, $P[X>x]$.
p: vector of probabilities.

Value

dig gives the density, pig gives the distribution function, qig gives the quantile function, and rig generates random deviates.

Invalid arguments will result in return value NaN, with a warning.

The length of the result is determined by n for rig.

Details

The inverse-Gaussian distribution has density given by $$f(x; a, b) = \frac{\sqrt{b}}{\sqrt{2\pi x^3}}\exp( -\frac{a}{2}x -\frac{b}{2x} + \sqrt{ab}),$$ where $x>0$ and $a,b>0$. In this parameterization, $E(X) = \sqrt{b}/\sqrt{a}$. See Tweedie (1957a, 1957b) for further details.

References

Tweedie, M. C. K. (1957a). "Statistical Properties of Inverse Gaussian Distributions I". Annals of Mathematical Statistics. 28 (2): 362–377. doi:10.1214/aoms/1177706964

Tweedie, M. C. K. (1957b). "Statistical Properties of Inverse Gaussian Distributions II". Annals of Mathematical Statistics. 28 (3): 696–705. doi:10.1214/aoms/1177706881

Examples

rig(100, a = 1, b = 1)
#>   [1] 0.9572548 0.5206169 1.2681461 0.4797213 0.7577269 3.7888009 1.7865166
#>   [8] 0.4946198 1.2474197 0.7415773 0.1896368 5.0856919 0.4952849 2.2866755
#>  [15] 0.1113017 2.5714447 1.9657381 1.9163777 1.0916878 0.5029270 1.8605299
#>  [22] 2.1373168 0.5127945 0.7622769 0.2723581 0.1074688 1.0646659 0.9720056
#>  [29] 0.3853628 4.3801731 2.2165500 0.7728686 1.2544806 2.9903736 1.5881800
#>  [36] 0.4964007 1.1668910 0.1990532 0.1513981 0.2455943 0.2466079 0.7062755
#>  [43] 0.3654105 0.3074057 0.2007869 0.6335298 0.5488414 1.4098436 0.7503542
#>  [50] 1.0460328 0.2983000 0.2564048 1.8425823 1.0157792 1.3456672 2.1760214
#>  [57] 1.0691253 0.3975510 0.1548133 1.1851614 1.5446015 0.4222253 1.3974503
#>  [64] 0.2743692 2.2350710 0.8131661 0.4329198 1.1496233 0.3880295 1.6086103
#>  [71] 0.6311459 1.7752646 0.3846843 0.1088839 0.6200793 0.4789168 1.7739017
#>  [78] 0.4080565 0.5951053 0.4625394 0.6501942 2.9418998 0.2883725 2.8822151
#>  [85] 1.4797474 0.7812484 0.2447756 0.2698109 0.2991567 0.2751294 0.9406372
#>  [92] 0.8039470 0.1696850 0.4746702 1.1946023 0.9306070 0.1478620 0.2871400
#>  [99] 1.3921724 1.0581139
pig(0.4, a = 1, b = 1)
#> [1] 0.2706137
qig(0.8, a = 1, b = 1)
#> [1] 1.447891
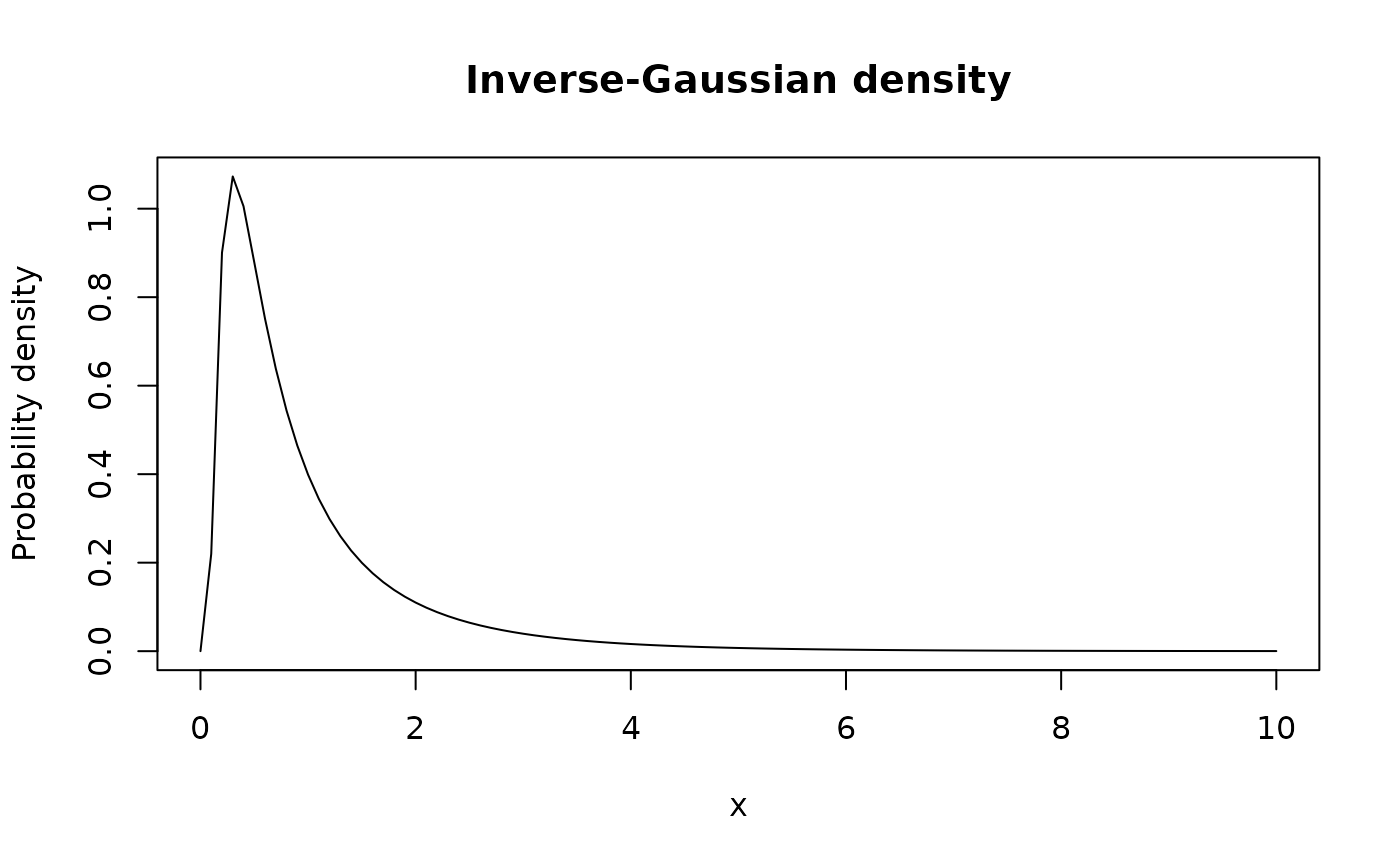
plot(function(x){dig(x, a = 1, b = 1)}, main =
"Inverse-Gaussian density", ylab = "Probability density",
xlim = c(0,10))