Prediction of an intrinsic Whittle-Matern model

The function is used for computing kriging predictions based on data \(Y_i = u(s_i) + \epsilon_i\), where \(\epsilon\) is mean-zero Gaussian measurement noise and \(u(s)\) is defined by an intrinsic SPDE as described in intrinsic.matern.operators().

Usage

# S3 method for class 'intrinsicCBrSPDEobj'
predict(
  object,
  A,
  Aprd,
  Y,
  sigma.e,
  mu = 0,
  compute.variances = FALSE,
  posterior_samples = FALSE,
  n_samples = 100,
  only_latent = FALSE,
  ...
)

Arguments

object

The covariance-based rational SPDE approximation, computed using intrinsic.matern.operators()

A

A matrix linking the measurement locations to the basis of the FEM approximation of the latent model.

Aprd

A matrix linking the prediction locations to the basis of the FEM approximation of the latent model.

Y

A vector with the observed data, can also be a matrix where the columns are observations of independent replicates of \(u\).

sigma.e

The standard deviation of the Gaussian measurement noise. Put to zero if the model does not have measurement noise.

mu

Expectation vector of the latent field (default = 0).

compute.variances

Set to also TRUE to compute the kriging variances.

posterior_samples

If TRUE, posterior samples will be returned.

n_samples

Number of samples to be returned. Will only be used if sampling is TRUE.

only_latent

Should the posterior samples be only given to the laten model?

...

further arguments passed to or from other methods.

Value

A list with elements

mean

The kriging predictor (the posterior mean of u|Y).

variance

The posterior variances (if computed).

Examples

if (requireNamespace("RSpectra", quietly = TRUE)) {
  x <- seq(from = 0, to = 10, length.out = 201)
  beta <- 1
  alpha <- 1
  kappa <- 1
  op <- intrinsic.matern.operators(
    kappa = kappa, tau = 1, alpha = alpha,
    beta = beta, loc_mesh = x, d = 1
  )
# Create some data
u <-  simulate(op)
sigma.e <- 0.1
obs.loc <- runif(n = 20, min = 0, max = 10)
A <- rSPDE.A1d(x, obs.loc)
Y <- as.vector(A %*% u + sigma.e * rnorm(20))

# compute kriging predictions at the FEM grid
A.krig <- rSPDE.A1d(x, x)
u.krig <- predict(op,
  A = A, Aprd = A.krig, Y = Y, sigma.e = sigma.e,
  compute.variances = TRUE
)

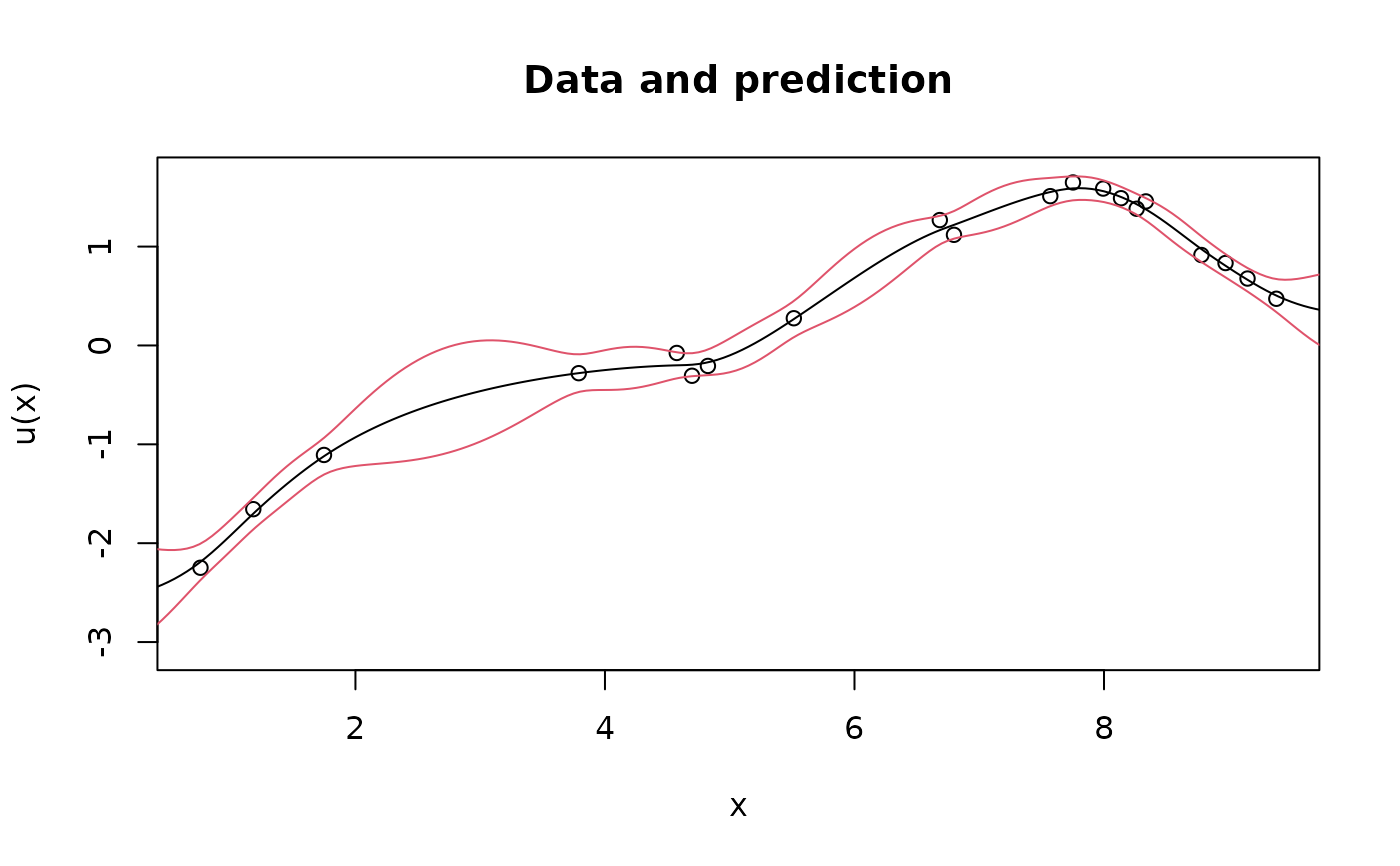
plot(obs.loc, Y,
  ylab = "u(x)", xlab = "x", main = "Data and prediction",
  ylim = c(
    min(u.krig$mean - 2 * sqrt(u.krig$variance)),
    max(u.krig$mean + 2 * sqrt(u.krig$variance))
  )
)
lines(x, u.krig$mean)
lines(x, u.krig$mean + 2 * sqrt(u.krig$variance), col = 2)
lines(x, u.krig$mean - 2 * sqrt(u.krig$variance), col = 2)
}