Skip to contents

An example with a river graph model

David Bolin, Alexandre B. Simas, and Jonas Wallin

Created: 2024-08-08. Last modified: 2024-12-13.

Source: vignettes/river_example.Rmd
river_example.Rmd

Introduction

In this vignette we explore how to build a directional graph model on a river network. The data is imported from the package SSN2.

Setting up the data

Here we take the data as is described in the Vignette of SSN2. We will use the geometry object from the SSN object to build the metricGraph object. We also load the observations and the relevant covariates. We assume that in the geometry object the lines are so that they go downwards along the river.

library(MetricGraph)
library(SSN2)

copy_lsn_to_temp()
path <- file.path(tempdir(), "MiddleFork04.ssn")

mf04p <- ssn_import(
  path = path,
  predpts = c("pred1km", "CapeHorn"),
  overwrite = TRUE
)

To create the graph, we simply pass the SSN object as edges. This will automatically extract the correct coordinate reference system (CRS). We have found that, typically, SSN objects do not require merges.

graph <- metric_graph$new(mf04p)

Observe that this already added, by default, the observations and edge weights contained in the SSN object:

dat <- graph$get_data()
graph$se
## NULL

and

graph$get_edge_weights()
## # A tibble: 163 × 17
##      rid    COMID GNIS_NAME   REACHCODE FTYPE FCODE AREAWTMAP   SLOPE rcaAreaKm2
##    <int>    <int> <chr>       <chr>     <chr> <int>     <dbl>   <dbl>      <dbl>
##  1     1 23519365 Bear Valle… 17060205… Stre… 46006     1001. 0.00274     4.65  
##  2     2 23519367 Bear Valle… 17060205… Stre… 46006     1002. 0.0071      0.839 
##  3     3 23519369 Bear Valle… 17060205… Stre… 46006     1003. 0.0036      3.91  
##  4     4 23519295 Bear Valle… 17060205… Stre… 46006     1010. 0.0147      0.0495
##  5     5 23519297 Bear Valle… 17060205… Stre… 46006     1007. 0.00568     5.02  
##  6     6 23519299 Bear Valle… 17060205… Stre… 46006     1003. 0.00104     0.992 
##  7     7 23519301 Bear Valle… 17060205… Stre… 46006     1006. 0.00271     1.46  
##  8     8 23519303 Bear Valle… 17060205… Stre… 46006     1009. 0.00055     0.597 
##  9     9 23519305 Bear Valle… 17060205… Stre… 46006     1009. 0.00026     1.32  
## 10    10 23519307 Bear Valle… 17060205… Stre… 46006     1009. 0.00042     0.865 
## # ℹ 153 more rows
## # ℹ 8 more variables: h2oAreaKm2 <dbl>, Length <dbl>, upDist <dbl>,
## #   areaPI <dbl>, afvArea <dbl>, netID <dbl>, netgeom <chr>, .weights <dbl>

Let us now turn the netID column of the data into a factor and store it in the graph:

graph$add_observations(graph$mutate(netID = as.factor(netID)), clear_obs=TRUE)
## Adding observations...
## The unit for edge lengths is km
## The current tolerance for removing distant observations is (in km): 3.16483618132507
## list()

We can now visualize the river and the data

graph$plot(data = "Summer_mn", vertex_size = 0.5)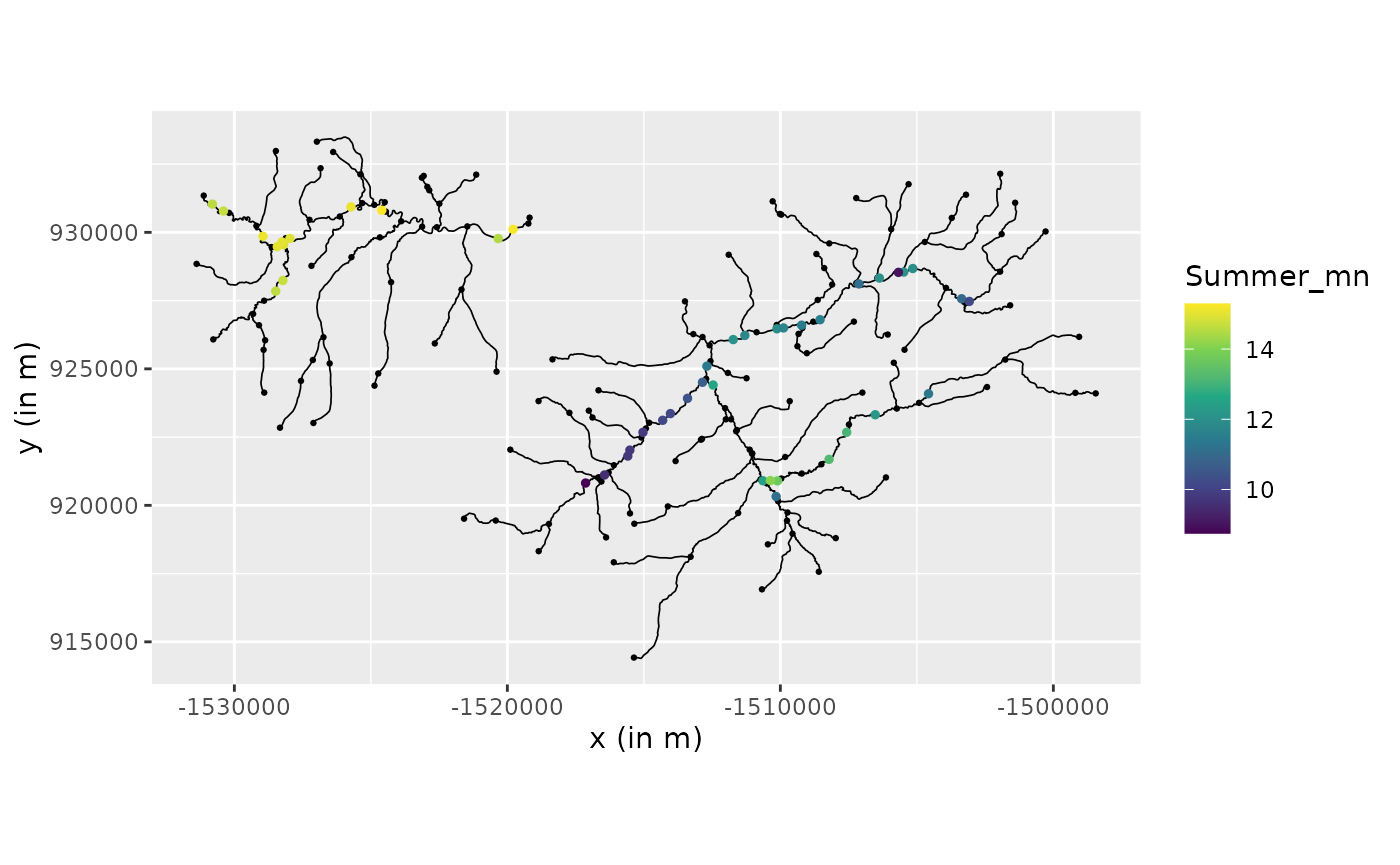

We can also visualize with an interactive plot by setting the type to mapview:

graph$plot(data = "Summer_mn", vertex_size = 0.5, type = "mapview")

Non directional models

We start with fitting the non directional models. First for alpha=1:

#fitting model with different smoothness
model.wm1 <- graph_lme(Summer_mn ~ SLOPE + netID, 
                          graph = graph, model = 'wm1')

and then for alpha=2:

model.wm2 <- graph_lme(Summer_mn ~   SLOPE + netID, 
                          graph = graph, model = 'wm2')

We also create the cross validation results to see how the models perform. Here we see that setting α=2\alpha=2, i.e. one time differential, has a much worse performance compared to α=1\alpha=1, i.e. continuous but non-differential.

cross.wm1 <-posterior_crossvalidation(model.wm1)
cross.wm2 <-posterior_crossvalidation(model.wm2)

cross.scores <- rbind(cross.wm1$scores,cross.wm2$scores)
print(cross.scores)
## # A tibble: 2 × 5
##   logscore  crps scrps   mae  rmse
##      <dbl> <dbl> <dbl> <dbl> <dbl>
## 1    0.784 0.276 0.715 0.362 0.504
## 2    0.807 0.285 0.731 0.373 0.521

Directional models

We now start with fitting various directional model. We start with having the “boundary condition” that at an edge the sum of the downward vertices should equal the upward vertices. That is if we have three edges e1,e2,e3e_1,e_2,e_3 connected so that e1,e2e_1,e_2 merge into e3e_3 we have at the vertex connecting them ue3(v)=ue1(v)+ue2(v). u_{e_3}(v) = u_{e_1}(v) + u_{e_2}(v). This is the default option in metricGraph and is created by:

res.wm1.dir <- graph_lme(Summer_mn ~   
                        SLOPE + netID, 
                        graph = graph, model = 'wmd1')

Here one can see a big improvement by adding using the directional model over the non directional.

cross.wm1.dir <-posterior_crossvalidation(res.wm1.dir)
cross.scores <- rbind(cross.scores,cross.wm1.dir$scores)
print(cross.scores)
## # A tibble: 3 × 5
##   logscore  crps scrps   mae  rmse
##      <dbl> <dbl> <dbl> <dbl> <dbl>
## 1    0.784 0.276 0.715 0.362 0.504
## 2    0.807 0.285 0.731 0.373 0.521
## 3    0.313 0.199 0.501 0.267 0.373

We could use other constraints. For instance in .. the authors used constraint not so the sum is equal but rather the variance of the in is constant which is obtained by ue3(v)=w1ue1(v)+w2ue2(v). u_{e_3}(v) = \sqrt{w_1}u_{e_1}(v) + \sqrt{w_2}u_{e_2}(v). here the weights are set by the edge weight h2oAreaKm2. To make this work in the metricgraph package one uses the following line

graph$set_edge_weights(directional_weights = 'h2oAreaKm2')
graph$setDirectionalWeightFunction(f_in = function(x){sqrt(x/sum(x))})
res.wm1.dir2 <- graph_lme(Summer_mn ~  SLOPE + netID, 
                                    graph = graph, model = 'wmd1')

Here we see a slight dip in performance but still much better than the symmetric version.

cross.wm1.dir2 <-posterior_crossvalidation(res.wm1.dir2)
cross.scores <- rbind(cross.scores,cross.wm1.dir2$scores)
print(cross.scores)
## # A tibble: 4 × 5
##   logscore  crps scrps   mae  rmse
##      <dbl> <dbl> <dbl> <dbl> <dbl>
## 1    0.784 0.276 0.715 0.362 0.504
## 2    0.807 0.285 0.731 0.373 0.521
## 3    0.313 0.199 0.501 0.267 0.373
## 4    0.440 0.218 0.567 0.309 0.395

We also want to generate predicitons over the river network this we do as follows:

graph$build_mesh(h = 0.1)
get_edge_cov <- graph$get_edge_weights()
 df_pred <- data.frame(edge_number = graph$mesh$PtE[,1],
                       distance_on_edge = graph$mesh$PtE[,2],
                       SLOPE = c(get_edge_cov[graph$mesh$PtE[,1],"SLOPE"]),
                       netID = c(get_edge_cov[graph$mesh$PtE[,1],"netID"]))
pred_alpha1 <- augment(res.wm1.dir , newdata = df_pred,
                        normalized = TRUE)
pred_alpha1$Temprature <- pred_alpha1$.fitted
pred_alpha1 %>% graph$plot(data = "Temprature", vertex_size = 0,
            type = "mapview")
## Warning: Found less unique colors (100) than unique zcol values (2529)! 
## Interpolating color vector to match number of zcol values.

Lets examine how things looks using the same residuals:

lm.data <- data.frame(Summer_mn = res.wm1.dir$graph$.__enclos_env__$private$data$Summer_mn,
                      SLOPE    =res.wm1.dir$graph$.__enclos_env__$private$data$SLOPE,
                      netID    =as.factor(res.wm1.dir$graph$.__enclos_env__$private$data$netID))
lm.model <- lm(Summer_mn ~ SLOPE +netID, data = lm.data )
res.wm1.dir$graph$.__enclos_env__$private$data$residuals = lm.model$residuals
res.wm1.dir2$graph$.__enclos_env__$private$data$residuals = lm.model$residuals

res.wm1.dir.res <- graph_lme(residuals ~ -1, 
                        graph = res.wm1.dir$graph, model = 'wmd1')
res.wm1.dir2.res <- graph_lme(residuals ~ -1, 
                                    graph = res.wm1.dir2$graph, model = 'wmd1')
cross.wm1.dir.res <-posterior_crossvalidation(res.wm1.dir.res)
cross.wm1.dir2.res <-posterior_crossvalidation(res.wm1.dir2.res)
cross.scores <- rbind(cross.wm1.dir.res$scores,cross.wm1.dir2.res$scores)
print(cross.scores)
## # A tibble: 2 × 5
##   logscore  crps scrps   mae  rmse
##      <dbl> <dbl> <dbl> <dbl> <dbl>
## 1    0.361 0.210 0.525 0.289 0.398
## 2    0.525 0.233 0.612 0.328 0.414
df_pred <- data.frame(edge_number = graph$mesh$PtE[,1],
                       distance_on_edge = graph$mesh$PtE[,2])
pred_alpha1.dir1.res <- augment(res.wm1.dir.res , newdata = df_pred,
                        normalized = TRUE)
pred_alpha1.dir2.res <- augment(res.wm1.dir2.res , newdata = df_pred,
                        normalized = TRUE)

pred_alpha1.dir1.res$.dresid <-- pred_alpha1.dir1.res$.fitted -pred_alpha1.dir2.res$.fitted 
pred_alpha1.dir1.res %>% graph$plot(data = ".dresid", vertex_size = 0,
            type = "mapview")
## Warning: Found less unique colors (100) than unique zcol values (2529)! 
## Interpolating color vector to match number of zcol values.