Skip to contents

Spatio-temporal Models on Compact Metric Graphs

David Bolin, Alexandre B. Simas, and Jonas Wallin

Created: 2024-10-23. Last modified: 2025-05-21.

Source: vignettes/spacetime.Rmd
spacetime.Rmd

Introduction

The MetricGraph package, combined with the rSPDE package, implements the following spatio-temporal model on compact metric graphs: du+γ(κ2+ρ⋅∇−Δ)αu=dWQ,on T×Γ d u + \gamma(\kappa^2 + \rho \cdot \nabla - \Delta)^{\alpha} u = dW_Q, \quad \text{on } T \times \Gamma where TT is a temporal interval, and Γ\Gamma is a compact metric graph. Here, κ>0\kappa > 0 is a spatial range parameter, ρ\rho is a drift parameter, and WQW_Q is a QQ-Wiener process with spatial covariance operator σ2(κ2−Δ)−β\sigma^2(\kappa^2 - \Delta)^{-\beta}, where σ2\sigma^2 is a variance parameter. The model has two smoothness parameters, α\alpha and β\beta, which are assumed to be integers. This model generalizes the spatio-temporal models introduced in Lindgren et al. (2024), where the generalization is to allow for drift and to allow for metric graphs as spatial domains. The model is implemented using a finite element discretization of the corresponding precision operator: σ−2(d+γ(κ2+κd/2ρ⋅∇−Δ)α)(κ2−Δ)β((d+γ(κ2−κd/2ρ⋅∇−Δ)α)) \sigma^{-2}(d + \gamma(\kappa^2 + \kappa^{d/2}\rho\cdot \nabla - \Delta)^{\alpha})(\kappa^2 - \Delta)^{\beta} ((d + \gamma(\kappa^2 - \kappa^{d/2}\rho\cdot \nabla - \Delta)^{\alpha})) in both space and time, following a similar discretization to Lindgren et al. (2024). This parameterization of the drift term, using ρκd/2\rho \kappa^{d/2} in place of the standard ρ\rho, is chosen to simplify the enforcement of theoretical bounds on the range of ρ\rho, ensuring that the equation remains well-posed and also providing numerical stability for finite-dimensional approximations.

Implementation Details

The function spacetime.operators(), provided by the rSPDE package, constructs the spatio-temporal precision matrix for models on metric graphs and enables interaction with the MetricGraph package. This function requires inputs that define the spatial structure via a MetricGraph object and the temporal domain through a vector of discretized time points. Key parameters like kappa and sigma control the range and variance of the field, respectively, whereas alpha and beta govern the smoothness of the field.

This function processes these inputs to create a spacetime.operators object containing the discretized precision matrix, covariance structure, and essential methods for model evaluation, simulation, and kriging on metric graphs.

library(sp)
library(rSPDE)
library(MetricGraph)

# Define graph edges
line1 <- Line(rbind(c(1, 0), c(0, 0)))
line2 <- Line(rbind(c(0, 0), c(0, 1)))
line3 <- Line(rbind(c(0, 0), c(0, -1)))
line4 <- Line(rbind(c(0, 1), c(1, 0)))
lines <- sp::SpatialLines(list(
  Lines(list(line1), ID="1"),
  Lines(list(line2), ID="2"),
  Lines(list(line3), ID="3"),
  Lines(list(line4), ID="4")
))

# Initialize metric graph
graph <- metric_graph$new(edges = lines)
graph$plot(direction = TRUE)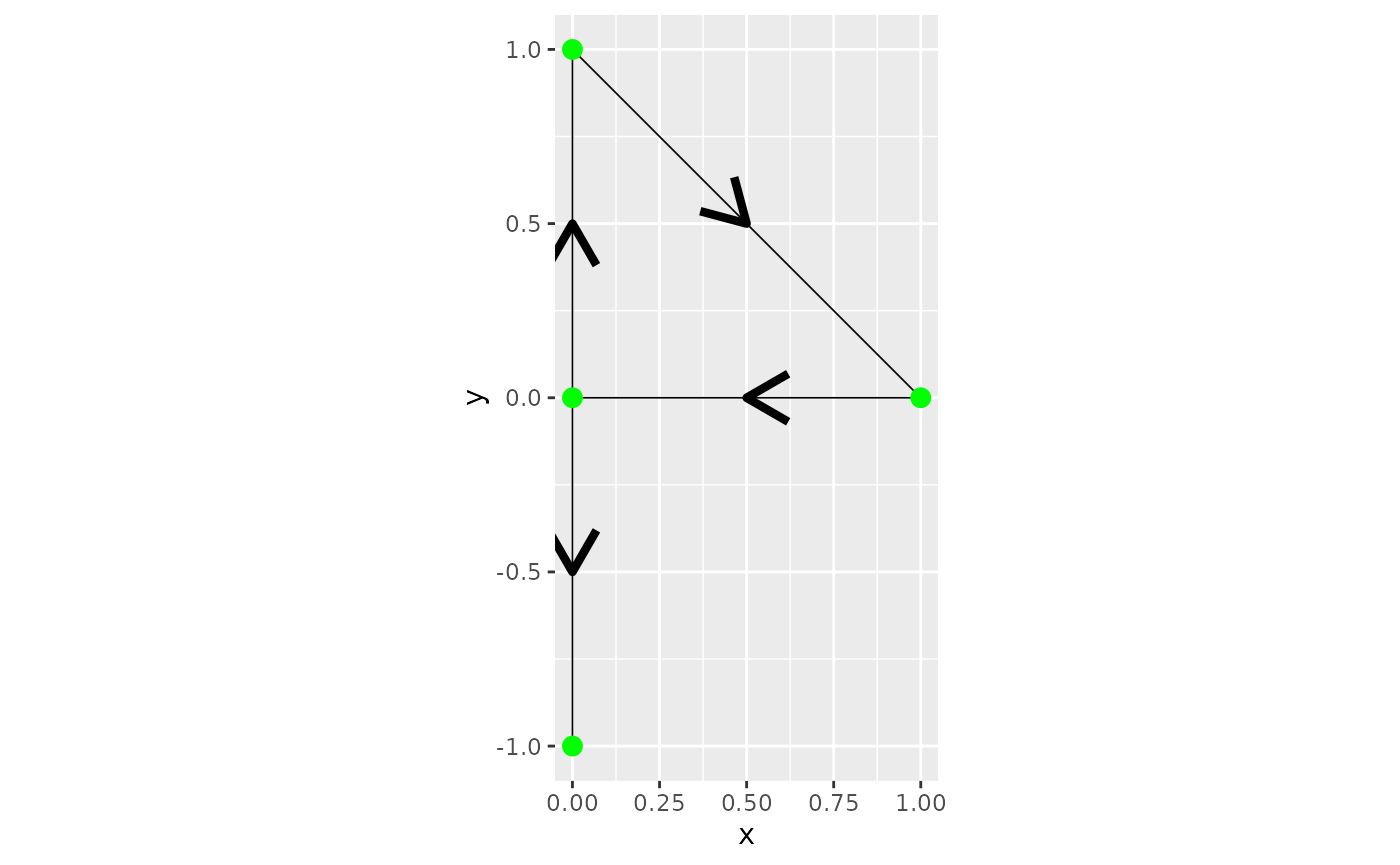


# Create finite element mesh and compute matrices
h <- 0.01
graph$build_mesh(h = h)
graph$compute_fem()

# Define model parameters and construct spatio-temporal operator
t <- seq(from = 0, to = 10, length.out = 31)
kappa <- 5
sigma <- 10
gamma <- 0.1
rho <- 0.3
alpha <- 1
beta <- 1

op <- spacetime.operators(graph = graph, time = t,
                          kappa = kappa, sigma = sigma, alpha = alpha,
                          beta = beta, rho = rho, gamma = gamma)
op$plot_covariances(t.ind = 15, s.ind = 50, t.shift = c(-1, 0, 1))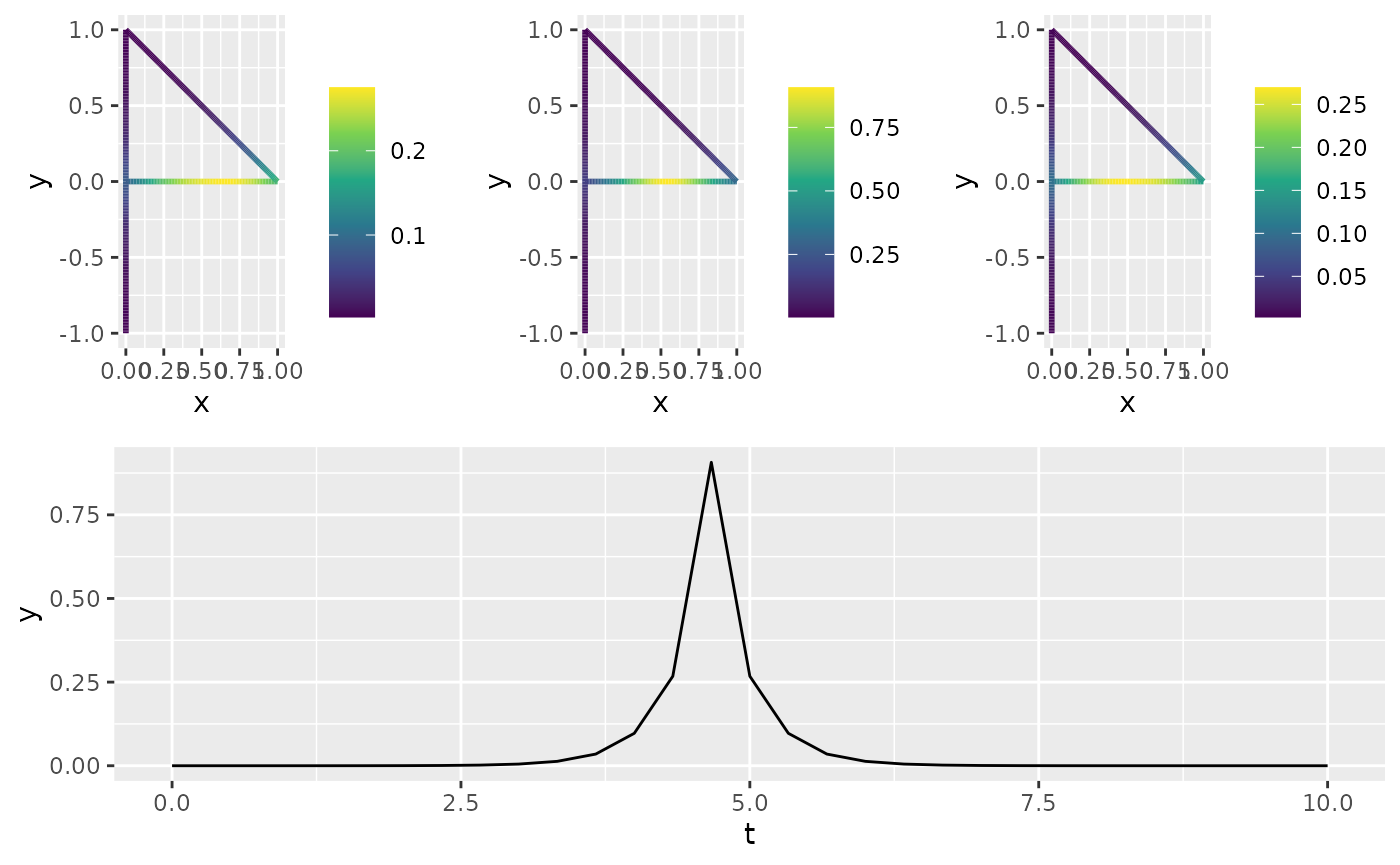

#> TableGrob (2 x 1) "arrange": 2 grobs
#>   z     cells    name            grob
#> 1 1 (1-1,1-1) arrange gtable[arrange]
#> 2 2 (2-2,1-1) arrange  gtable[layout]
#> TableGrob (2 x 1) "arrange": 2 grobs
#>   z     cells    name            grob
#> 1 1 (1-1,1-1) arrange gtable[arrange]
#> 2 2 (2-2,1-1) arrange  gtable[layout]

Simulating Observations and Estimating Parameters 

# Simulate data
x <- simulate(op, nsim = 1) 

n.obs <- 500
PtE <- cbind(sample(1:graph$nE, size = n.obs, replace = TRUE), runif(n.obs))
t.obs <- max(t) * runif(n.obs)

# including vertices of degree 1 in the A matrix
A <- op$make_A(PtE, t.obs, include_deg1 = TRUE)
sigma.e <- 0.01
Y <- as.vector(A %*% x + sigma.e * rnorm(n.obs))
df <- data.frame(y = as.matrix(Y), edge_number = PtE[,1], 
                        distance_on_edge = PtE[,2], 
                        time = t.obs)
graph$add_observations(data = df, normalized=TRUE,
                              group = "time")

# Estimate model parameters using rspde_lme
res <- rspde_lme(y ~ 1, loc_time = "time",
                 model = op, 
                 parallel = TRUE)

# Display summary
summary(res)
#> 
#> Latent model - Spatio-temporal with alpha =  1 , beta =  1
#> 
#> Call:
#> rspde_lme(formula = y ~ 1, loc_time = "time", model = op, parallel = TRUE)
#> 
#> Fixed effects:
#>             Estimate Std.error z-value Pr(>|z|)
#> (Intercept)  0.01251   0.01420   0.881    0.379
#> 
#> Random effects:
#>               Estimate Std.error z-value
#> kappa          5.08240   0.31330  16.222
#> sigma         10.61095   1.14281   9.285
#> gamma          0.10780   0.01255   8.587
#> rho            0.18396   8.02863   0.023
#> alpha (fixed)  1.00000        NA      NA
#> beta (fixed)   1.00000        NA      NA
#> 
#> Measurement error:
#>          Estimate Std.error z-value
#> std. dev 0.011327  0.002193   5.164
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 
#> 
#> Log-Likelihood:  -38.3092 
#> Number of function calls by 'optim' = 82
#> Optimization method used in 'optim' = L-BFGS-B
#> 
#> Time used to:     fit the model =  53.79679 secs 
#>   set up the parallelization = 19.35974 secs

# Compare estimated results with true values
results <- data.frame(kappa = c(kappa, res$coeff$random_effects[1]), 
                      sigma = c(sigma, res$coeff$random_effects[2]),
                      gamma = c(gamma, res$coeff$random_effects[3]), 
                      rho = c(rho, res$coeff$random_effects[4]),
                      sigma.e = c(sigma.e, res$coeff$measurement_error),
                      intercept = c(0, res$coeff$fixed_effects),
                      row.names = c("True", "Estimate"))
                      
print(results)
#>           kappa    sigma     gamma       rho    sigma.e  intercept
#> True     5.0000 10.00000 0.1000000 0.3000000 0.01000000 0.00000000
#> Estimate 5.0824 10.61095 0.1077964 0.1839591 0.01132677 0.01250703

inlabru Implementation

We now proceed with the inlabru implementation. First, we create a temporal mesh:

library(INLA)
library(inlabru)
library(fmesher)
mesh_time <- fm_mesh_1d(t)
st_graph <- rspde.spacetime(mesh_space = graph, 
                                    mesh_time = mesh_time, 
                                    alpha = 1, beta = 1)

We define the data object by using the graph_data_rspde() function with bru set to TRUE:

st_data_bru <- graph_data_rspde(st_graph, bru = TRUE)

Next, we define the model component for inlabru, where we pass a list with two elements: space, which is given by the spatial locations (cbind(.edge_number, .distance_on_edge)), and time, which is given by the time points.

cmp_graph <- y ~ 1 + field(list(
                        space = cbind(.edge_number, .distance_on_edge), 
                                    time = time), 
                                    model = st_graph)

Fit the model by passing st_data_bru to the data argument:

bru_fit_graph <- bru(cmp_graph, data = st_data_bru[["data"]])

Compare the estimated parameters with the true values:

param_st <- transform_parameters_spacetime(bru_fit_graph$summary.hyperpar$mean[2:6], 
                                            st_graph)

results <- data.frame(kappa = c(kappa,  param_st[[1]]), 
                      sigma = c(sigma,  param_st[[2]]),
                      gamma = c(gamma,  param_st[[3]]), 
                      rho = c(rho, param_st[[4]]),
                      sigma.e = c(sigma.e, sqrt(1/bru_fit_graph$summary.hyperpar$mean[1])),
                      intercept = c(0, bru_fit_graph$summary.fixed$mean),
                      row.names = c("True", "Estimate"))
                      
print(results)
#>             kappa    sigma     gamma       rho    sigma.e  intercept
#> True     5.000000 10.00000 0.1000000 0.3000000 0.01000000 0.00000000
#> Estimate 5.117334 10.76211 0.1088906 0.1083284 0.01028202 0.01261628

Fitting Model with Replicates in inlabru

We will now simulate from the same model, but this time with replicates. We will assume we have 10 replicates.

Let us start by simulating the field:

n_rep = 10
x <- simulate(op, nsim = n_rep) 

n.obs <- 500
PtE <- cbind(sample(1:graph$nE, size = n.obs, replace = TRUE), runif(n.obs))
t.obs <- max(t) * runif(n.obs)
A <- op$make_A(PtE, t.obs, include_deg1 = TRUE)
sigma.e <- 0.01
Y <- as.vector(A %*% x + sigma.e * rnorm(n.obs))
df <- data.frame(y = as.matrix(Y), edge_number = PtE[,1], 
                        distance_on_edge = PtE[,2], time = t.obs,
                        repl = rep(1:n_rep, each = n.obs))

graph_rep <- graph$clone()

We add the observations into the metric graph object. Observe that this time we have two grouping variables, time and repl. We need grouping variables whenever we want to allow the storage of different observations at the exact same location.

graph_rep$add_observations(data = df, normalized=TRUE, 
                    clear_obs = TRUE, group = c("time", "repl"))
#> Adding observations...
#> Assuming the observations are normalized by the length of the edge.

We now create the rSPDE model object:

st_graph_repl <- rspde.spacetime(mesh_space = graph_rep, 
                                mesh_time = mesh_time, 
                                alpha = 1, beta = 1)

We create the data object by using the graph_data_rspde() function, setting bru to TRUE and specifying repl_col:

st_data_bru_repl <- graph_data_rspde(st_graph_repl, 
                                  repl = ".all",
                                  repl_col = "repl",
                                  bru = TRUE)

Next, we create the inlabru component by also passing the replicate argument with the repl element of the object returned by graph_data_rspde():

cmp_graph_repl <- y ~ 1 + field(list(space = cbind(.edge_number, .distance_on_edge), 
                                time = time),
                                model = st_graph_repl,
                                replicate = st_data_bru_repl[["repl"]]
                                )

Fit the model passing st_data_bru_repl to the data argument:

bru_fit_graph_repl <- bru(cmp_graph_repl, 
                      data = st_data_bru_repl[["data"]])

Compare the estimated parameters with the true values:

param_st_repl <- transform_parameters_spacetime(
                              bru_fit_graph_repl$summary.hyperpar$mean[2:6], 
                              st_graph_repl)

results_repl <- data.frame(kappa = c(kappa,  param_st_repl[[1]]), 
                      sigma = c(sigma,  param_st_repl[[2]]),
                      gamma = c(gamma,  param_st_repl[[3]]), 
                      rho = c(rho, param_st_repl[[4]]),
                      sigma.e = c(sigma.e, sqrt(1/bru_fit_graph_repl$summary.hyperpar$mean[1])),
                      intercept = c(0, bru_fit_graph_repl$summary.fixed$mean),
                      row.names = c("True", "Estimate"))
                      
print(results_repl)
#>            kappa    sigma      gamma       rho     sigma.e   intercept
#> True     5.00000 10.00000 0.10000000 0.3000000 0.010000000  0.00000000
#> Estimate 5.17993 10.39482 0.09850795 0.2805618 0.007509316 -0.02281056

Example: Setting bounded_rho = FALSE

The bounded_rho parameter in rspde.spacetime() ensures that ρ\rho stays within a range that guarantees numerical stability and well-posedness. However, in some cases, better fits can be achieved by setting bounded_rho = FALSE. Below, we show how to modify the model to handle this case.

Using rspde_lme()

Here we set bounded_rho = FALSE when creating the spatio-temporal operator and fit the model using rspde_lme():

# Create the spatio-temporal operator with bounded_rho = FALSE
op_unbounded <- spacetime.operators(
  graph = graph,
  time = t,
  kappa = kappa,
  sigma = sigma,
  alpha = alpha,
  beta = beta,
  rho = rho,
  gamma = gamma,
  bounded_rho = FALSE
)

# Fit the model using rspde_lme
res <- rspde_lme(y ~ 1, loc_time = "time", model = op_unbounded, parallel = TRUE)

Comparing Results 

# Compare results for rspde_lme
results <- data.frame(
  kappa = c(kappa, res$coeff$random_effects[1]),
  sigma = c(sigma, res$coeff$random_effects[2]),
  gamma = c(gamma, res$coeff$random_effects[3]),
  rho = c(rho, res$coeff$random_effects[4]),
  sigma.e = c(sigma.e, res$coeff$measurement_error),
  intercept = c(0, res$coeff$fixed_effects),
  row.names = c("True", "Estimate")
)

print(results)
#>             kappa    sigma     gamma       rho    sigma.e  intercept
#> True     5.000000 10.00000 0.1000000 0.3000000 0.01000000 0.00000000
#> Estimate 5.082678 10.61166 0.1077996 0.1840976 0.01132633 0.01251262

Using inlabru

Here we set bounded_rho = FALSE when creating the spatio-temporal operator and prepare data for inlabru:

# Create the spatio-temporal operator for inlabru
st_graph_unbounded <- rspde.spacetime(
  mesh_space = graph,
  mesh_time = mesh_time,
  alpha = 1,
  beta = 1,
  bounded_rho = FALSE
)

# Prepare data for inlabru
st_data_bru_unbounded <- graph_data_rspde(
  st_graph_unbounded,
  bru = TRUE
)

# Define inlabru component with unbounded rho
cmp_graph_unbounded <- y ~ 1 + field(
  list(
    space = cbind(.edge_number, .distance_on_edge),
    time = time
  ),
  model = st_graph_unbounded
)

Fitting the Model with inlabru 

bru_fit_graph_unbounded <- bru(cmp_graph_unbounded, data = st_data_bru_unbounded[["data"]])

Comparing Results 

# Transform parameters and compare results
param_st_unbounded <- transform_parameters_spacetime(
  bru_fit_graph_unbounded$summary.hyperpar$mean[2:6],
  st_graph_unbounded
)

results_unbounded <- data.frame(
  kappa = c(kappa, param_st_unbounded[[1]]),
  sigma = c(sigma, param_st_unbounded[[2]]),
  gamma = c(gamma, param_st_unbounded[[3]]),
  rho = c(rho, param_st_unbounded[[4]]),
  sigma.e = c(sigma.e, sqrt(1 / bru_fit_graph_unbounded$summary.hyperpar$mean[1])),
  intercept = c(0, bru_fit_graph_unbounded$summary.fixed$mean),
  row.names = c("True", "Estimate")
)

print(results_unbounded)
#>             kappa    sigma     gamma       rho    sigma.e  intercept
#> True     5.000000 10.00000 0.1000000 0.3000000 0.01000000 0.00000000
#> Estimate 5.105099 10.74732 0.1086507 0.1850006 0.01068344 0.01264715

INLA Implementation (Added for Completeness)

Note: While it is possible to fit the model directly using INLA, we strongly recommend utilizing the inlabru implementation. Its higher-level interface and enhanced functionalities provide a more user-friendly and robust experience, especially for those with less experience in advanced modeling.

Fitting the Model with INLA

First, we create the temporal mesh and spatio-temporal graph:

library(INLA)
library(fmesher)
mesh_time <- fm_mesh_1d(t)
st_graph <- rspde.spacetime(mesh_space = graph, 
                                    mesh_time = mesh_time, 
                                    alpha = 1, beta = 1)

We define the data object by using the graph_data_rspde() function with bru set to FALSE:

st_data_inla <- graph_data_rspde(st_graph, name = "field", time = "time", bru = FALSE)

Now we create the inla.stack object. The st_data_inla contains the dataset as the data component, the index as the index component, and the so-called A matrix as the basis component. We will now create the stack using these components:

stk.dat <- inla.stack(
  data = st_data_inla[["data"]], 
  A = st_data_inla[["basis"]],
  effects =
    c(st_data_inla[["index"]],
      list(Intercept = 1))
  )

Finally, we create the formula object and fit the model:

f_st <- y ~ -1 + Intercept + f(field, model = st_graph)

rspde_fit <- inla(f_st, data = inla.stack.data(stk.dat),
  control.inla = list(int.strategy = "eb"),
  control.predictor = list(A = inla.stack.A(stk.dat), compute = TRUE),
  num.threads = "1:1"
)

Let us compare the fitted values with the true values:

param_st <- transform_parameters_spacetime(rspde_fit$summary.hyperpar$mean[2:6], 
                                            st_graph)

results <- data.frame(kappa = c(kappa,  param_st[[1]]), 
                      sigma = c(sigma,  param_st[[2]]),
                      gamma = c(gamma,  param_st[[3]]), 
                      rho = c(rho, param_st[[4]]),
                      sigma.e = c(sigma.e, sqrt(1/rspde_fit$summary.hyperpar$mean[1])),
                      intercept = c(0, rspde_fit$summary.fixed$mean),
                      row.names = c("True", "Estimate"))
                      
print(results)
#>             kappa    sigma     gamma        rho    sigma.e  intercept
#> True     5.000000 10.00000 0.1000000 0.30000000 0.01000000 0.00000000
#> Estimate 5.101234 10.96275 0.1118911 0.02808996 0.01041762 0.01258624

Fitting Model with Replicates in INLA

We will now simulate from the same model, but this time with replicates.

Let us create the data object for INLA:

st_data_inla_repl <- graph_data_rspde(st_graph_repl, 
                                  repl = ".all",
                                  repl_col = "repl",
                                  time = "time",
                                  bru = FALSE)

Let us now create the corresponding inla.stack object:

st_dat_rep <- inla.stack(
  data = st_data_inla_repl[["data"]],
  A = st_data_inla_repl[["basis"]],
  effects = c(st_data_inla_repl[["index"]],
          list(Intercept = 1))
)

Now, we can create the formula object and fit the model:

f_st_rep <-
  y ~ -1 + Intercept + f(field,
    model = st_graph_repl,
    replicate = field.repl
  )

rspde_fit_rep <-
  inla(f_st_rep,
    data = inla.stack.data(st_dat_rep),
    control.predictor =
      list(A = inla.stack.A(st_dat_rep))
  )

Let us compare the fitted values with the true values:

param_st_rep <- transform_parameters_spacetime(rspde_fit_rep$summary.hyperpar$mean[2:6], 
                                            st_graph)

results_inla_repl <- data.frame(kappa = c(kappa,  param_st_rep[[1]]), 
                      sigma = c(sigma,  param_st_rep[[2]]),
                      gamma = c(gamma,  param_st_rep[[3]]), 
                      rho = c(rho,  param_st_rep[[4]]),
                      sigma.e = c(sigma.e, sqrt(1/rspde_fit_rep$summary.hyperpar$mean[1])),
                      intercept = c(0, rspde_fit_rep$summary.fixed$mean),
                      row.names = c("True", "Estimate"))
                      
print(results_inla_repl)
#>             kappa    sigma    gamma        rho     sigma.e   intercept
#> True     5.000000 10.00000 0.100000 0.30000000 0.010000000  0.00000000
#> Estimate 5.152535 10.42789 0.100871 0.08205531 0.009895787 -0.01459013

References

Lindgren, Finn, Haakon Bakka, David Bolin, Elias Krainski, and Håvard Rue. 2024. “A Diffusion-Based Spatio-Temporal Extension of Gaussian Matérn Fields.” SORT Statistics and Operations Research Transactions 48 (1): 3–66.