Skip to contents

An example with multiple likelihoods in INLA and inlabru

David Bolin, Alexandre B. Simas, and Jonas Wallin

Created: 2024-07-06. Last modified: 2024-12-13.

Source: vignettes/multi_likelihood.Rmd
multi_likelihood.Rmd

Introduction

In this vignette we will show how to fit a model with multiple likelihoods with our INLA and inlabru implementations. We will consider the following model: Y1i=β1+u(si)+ε1i,Y_{1i} = \beta_1 + u(s_i) + \varepsilon_{1i},Y2i=β2+u(si)+ε2i,Y_{2i} = \beta_2 + u(s_i) + \varepsilon_{2i}, where s1,…,sns_1,\ldots,s_n are locations on a compact metric graph Γ\Gamma, u(⋅)u(\cdot) is a Whittle–Matérn field with alpha=1, i=1,…,ni=1,\ldots,n, ϵ11,…,ϵ1n\epsilon_{11},\ldots, \epsilon_{1n} are i.i.d. random variables following N(0,σ12)N(0, \sigma_1^2), and ϵ21,…,ϵ2n\epsilon_{21}, \ldots, \epsilon_{2n} are i.i.d. random variables following N(0,σ22)N(0,\sigma_2^2), finally, we will take n=400n=400.

A toy dataset

We will start by generating the dataset. Let us load the MetricGraph package and create the metric graph:

library(MetricGraph)

edge1 <- rbind(c(0,0),c(1,0))
edge2 <- rbind(c(0,0),c(0,1))
edge3 <- rbind(c(0,1),c(-1,1))
theta <- seq(from=pi,to=3*pi/2,length.out = 20)
edge4 <- cbind(sin(theta),1+ cos(theta))
edges = list(edge1, edge2, edge3, edge4)
graph <- metric_graph$new(edges = edges)

Let us add 100 random locations in each edge where we will have observations:

obs_per_edge <- 100
obs_loc <- NULL
for(i in 1:(graph$nE)) {
  obs_loc <- rbind(obs_loc,
                   cbind(rep(i,obs_per_edge), 
                   runif(obs_per_edge)))
}

We will now sample in these observation locations and plot the latent field:

sigma <- 2
alpha <- 1
nu <- alpha - 0.5
r <- 0.15 # r stands for range

u <- sample_spde(range = r, sigma = sigma, alpha = alpha,
                 graph = graph, PtE = obs_loc)
graph$plot(X = u, X_loc = obs_loc)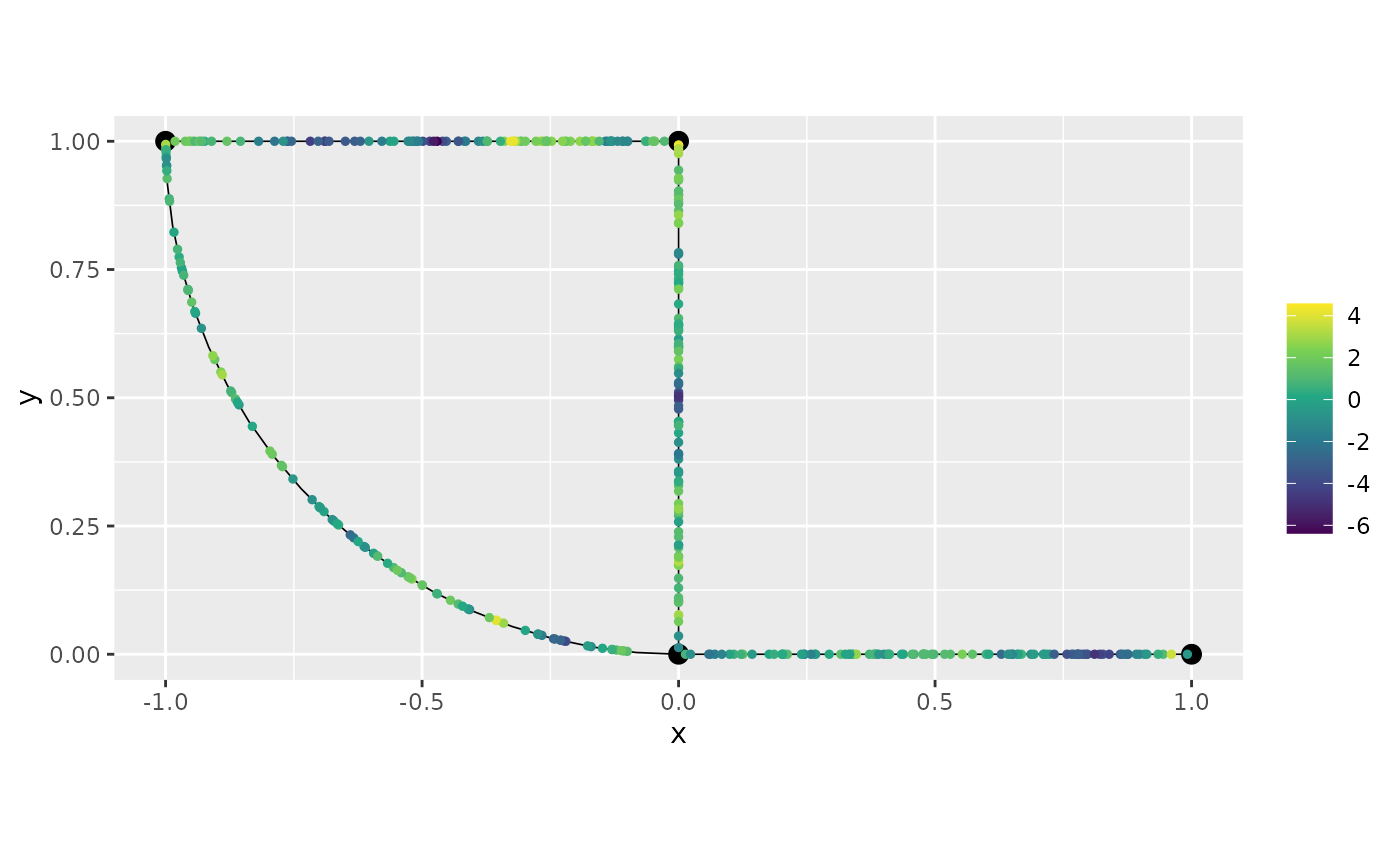

Let us now generate the observed responses for both likelihoods, which we will call, respectively, y1 and y2. We will also plot the observed responses on the metric graph.

beta1 = 2
beta2 = -2
n_obs <- length(u)
sigma1.e <- 0.2
sigma2.e <- 0.5

y1 <- beta1 + u + sigma1.e * rnorm(n_obs)
y2 <- beta2 + u + sigma2.e * rnorm(n_obs)

Let us plot the observations from y1:

graph$plot(X = y1, X_loc = obs_loc)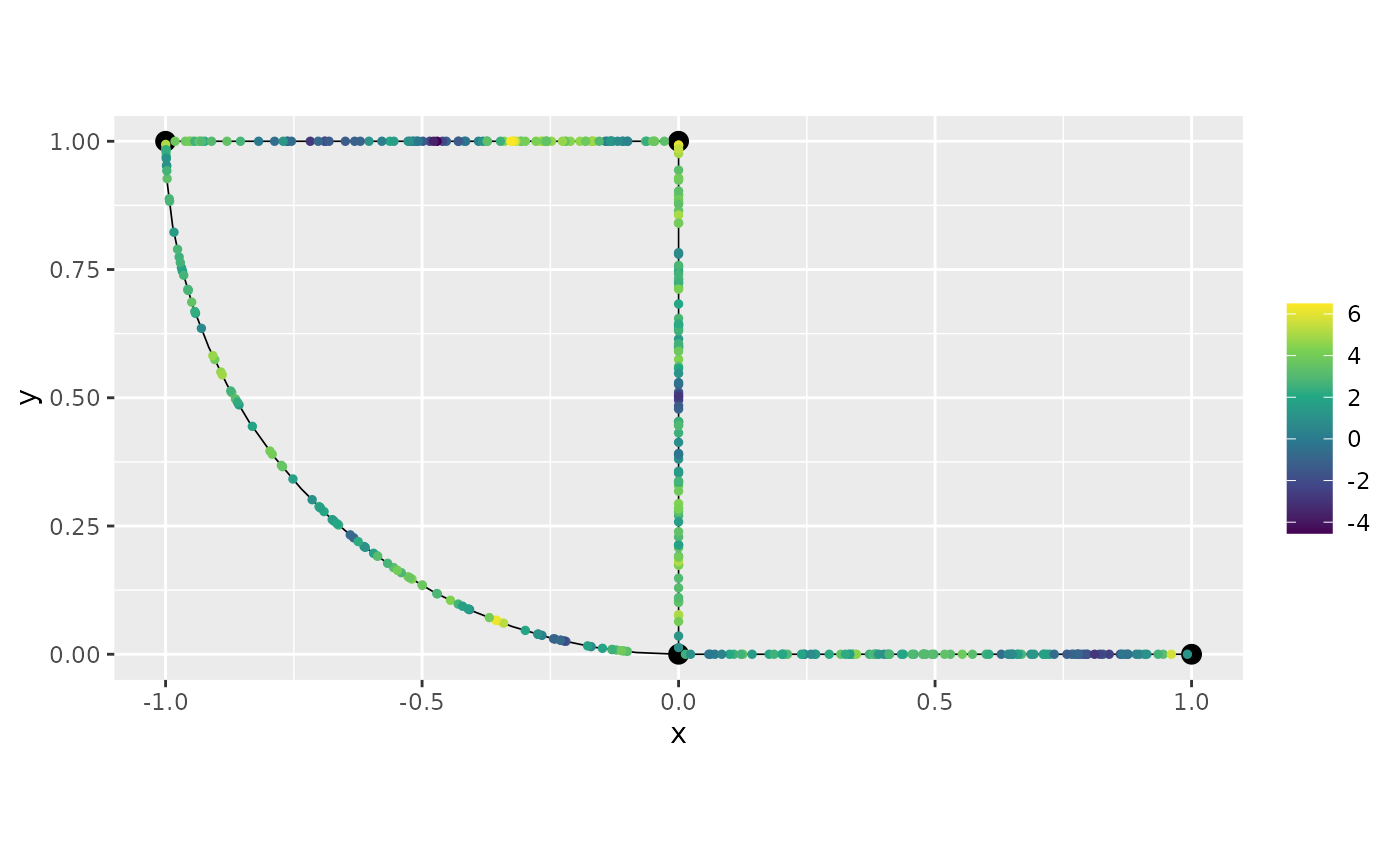

and from y2:

graph$plot(X = y2, X_loc = obs_loc)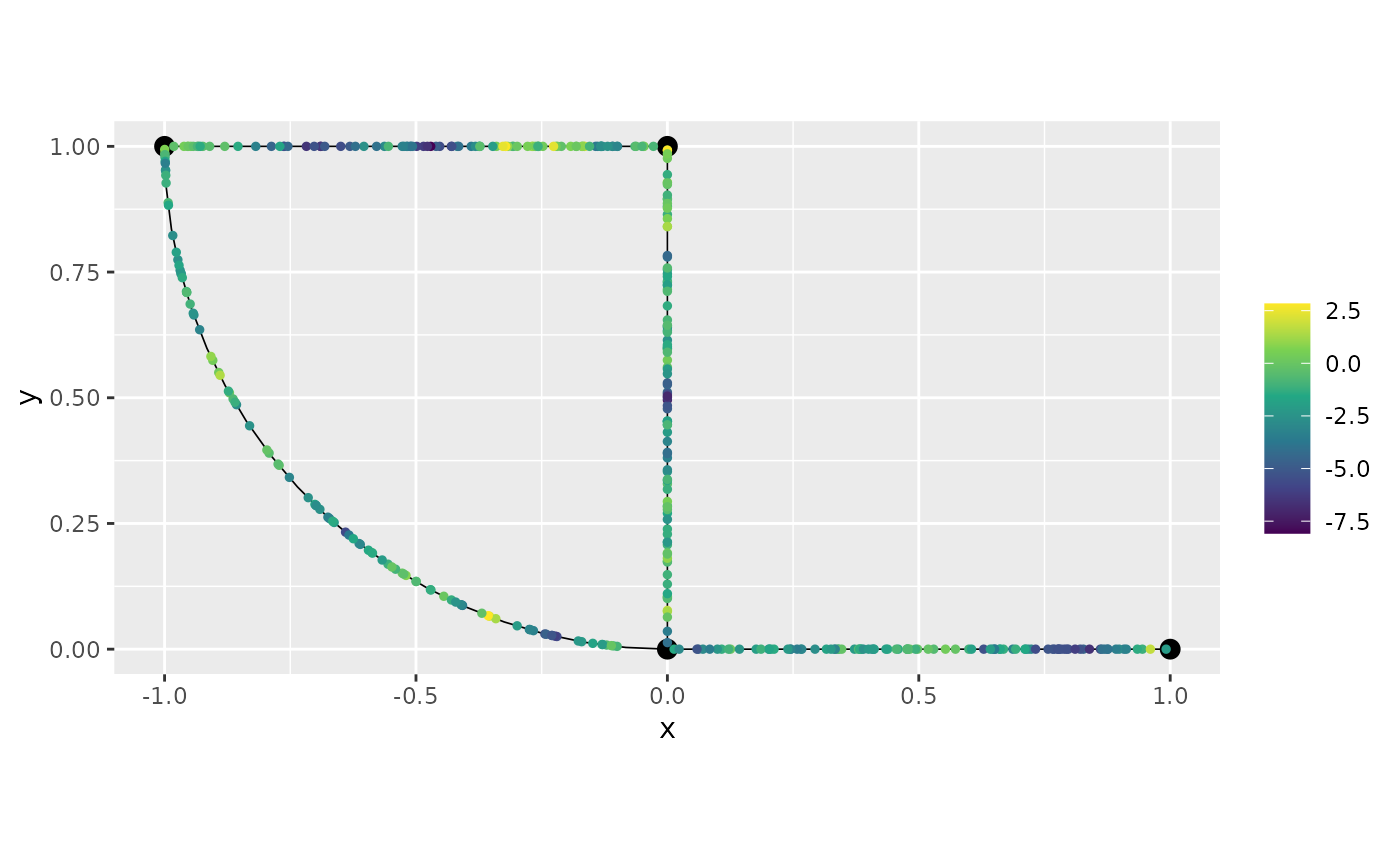

Fitting models with multiple likelihoods in R-INLA

We are now in a position to fit the model with our R-INLA implementation. To this end, we need to add the observations to the graph, which we will do with the add_observations() method. We will create a column on the data.frame to indicate which likelihood the observed variable belongs to. We will also the intercepts as columns.

df_graph1 <- data.frame(y = y1, intercept_1 = 1, intercept_2 = NA,
                        edge_number = obs_loc[,1],
                        distance_on_edge = obs_loc[,2],
                        likelihood = 1)
df_graph2 <- data.frame(y = y2, intercept_1 = NA,
                        intercept_2 = 1,
                        edge_number = obs_loc[,1],
                        distance_on_edge = obs_loc[,2],
                        likelihood = 2)      
df_graph <- rbind(df_graph1, df_graph2)

Let us now add the observations and set the likelihood column as group:

graph$add_observations(data=df_graph, normalized=TRUE, group = "likelihood")
## list()
graph$plot(data="y")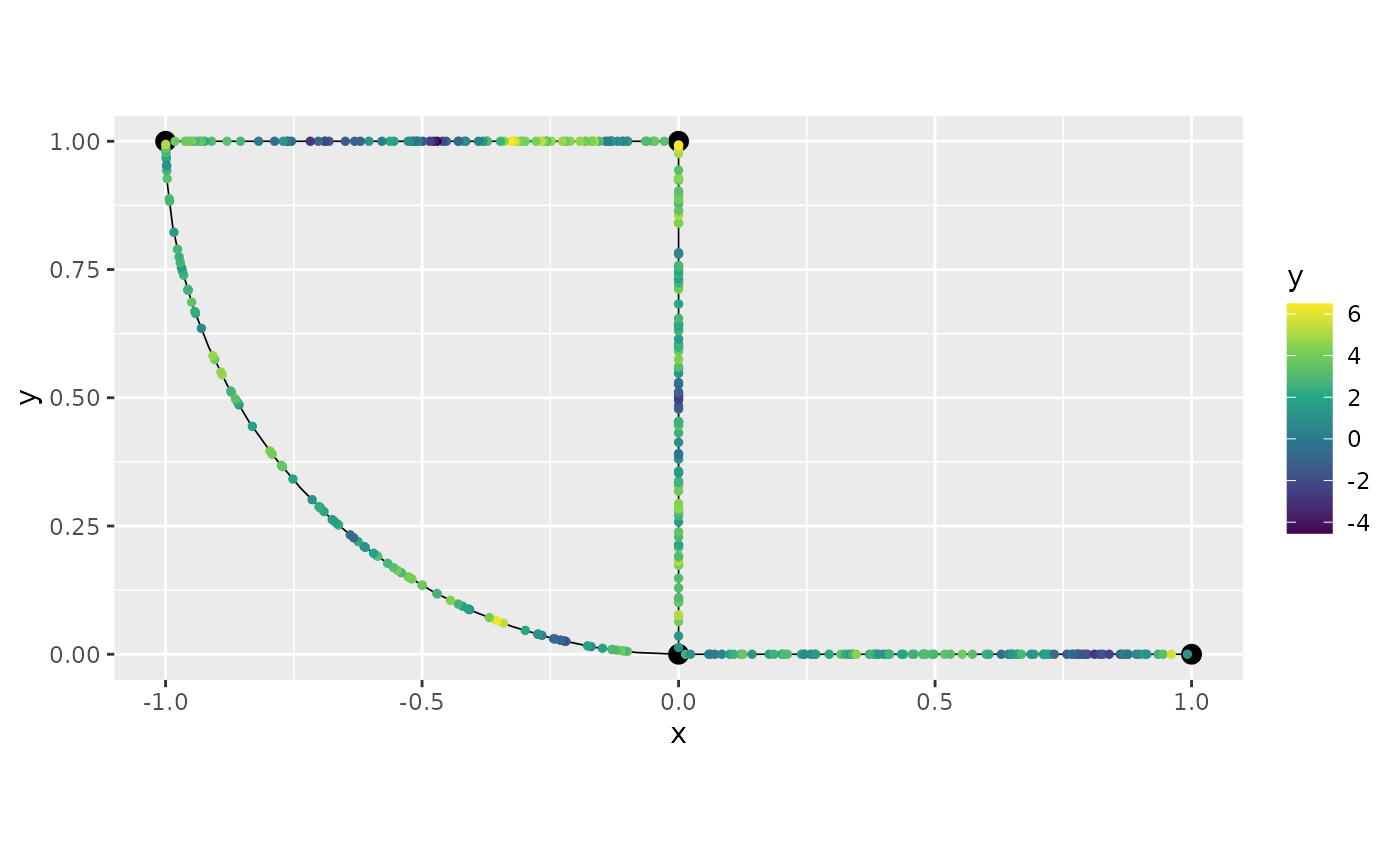

Now, we load the R-INLA package and create the inla model object with the graph_spde function. By default we have alpha=1.

library(INLA)
spde_model <- graph_spde(graph)

Now, we need to create the data object with the graph_data_spde() function, in which we need to provide a name for the random effect, which we will call field, and we need to provide the covariates. We also need to pass the column that contains the number of the likelihood for the data

data_spde <- graph_data_spde(graph_spde = spde_model, 
                name = "field", likelihood_col = "likelihood",
                resp_col = "y",
                covariates = c("intercept_1", "intercept_2"))

The remaining is standard in R-INLA. We create the formula object and the inla.stack objects with the inla.stack() function.

Let us start by creating the formula:

f.s <- y ~ -1 + f(intercept_1, model = "linear") + 
        f(intercept_2, model = "linear") + 
        f(field, model = spde_model)

Let us now create the inla.stack objects, one for each likelihood. To such an end, we simply supply the data in data_spde obtained from using graph_data_spde:

stk_dat1 <- inla.stack(data = data_spde[[1]][["data"]], 
                        A = data_spde[[1]][["basis"]], 
                        effects = data_spde[[1]][["index"]]
    )
stk_dat2 <- inla.stack(data = data_spde[[2]][["data"]], 
                        A = data_spde[[2]][["basis"]], 
                        effects = data_spde[[2]][["index"]]
    )
stk_dat <- inla.stack(stk_dat1, stk_dat2)

Now, we use the inla.stack.data():

data_stk <- inla.stack.data(stk_dat)

Finally, we fit the model:

spde_fit <- inla(f.s, family = c("gaussian", "gaussian"), 
    data = data_stk, control.predictor=list(A=inla.stack.A(stk_dat)),
                               num.threads = "1:1")

Let us now obtain the estimates in the original scale by using the spde_metric_graph_result() function, then taking a summary():

spde_result <- spde_metric_graph_result(spde_fit, "field", spde_model)

summary(spde_result)
##           mean       sd 0.025quant 0.5quant 0.975quant     mode
## sigma 1.937700 0.180833   1.612950 1.926410   2.318850 1.889720
## range 0.134568 0.027153   0.090397 0.131344   0.196619 0.124828

We will now compare the means of the estimated values with the true values:

  result_df <- data.frame(
    parameter = c("std.dev", "range"),
    true = c(sigma, r),
    mean = c(
      spde_result$summary.sigma$mean,
      spde_result$summary.range$mean
    ),
    mode = c(
      spde_result$summary.sigma$mode,
      spde_result$summary.range$mode
    )
  )
  print(result_df)
##   parameter true      mean      mode
## 1   std.dev 2.00 1.9377009 1.8897173
## 2     range 0.15 0.1345677 0.1248283

Let us now look at the estimates of the measurement errors and compare with the true ones:

meas_err_df <- data.frame(
    parameter = c("sigma1.e", "sigma2.e"),
    true = c(sigma1.e, sigma2.e),
    mean = sqrt(1/spde_fit$summary.hyperpar$mean[1:2]),
    mode = sqrt(1/spde_fit$summary.hyperpar$mode[1:2])
  )
print(meas_err_df)
##   parameter true     mean      mode
## 1  sigma1.e  0.2 0.223109 0.2377587
## 2  sigma2.e  0.5 0.496475 0.4987251

Finally, let us look at the estimates of the intercepts:

intercept_df <- data.frame(
    parameter = c("beta1", "beta2"),
    true = c(beta1, beta2),
    mean = spde_fit$summary.fixed$mean,
    mode = spde_fit$summary.fixed$mode
  )
print(intercept_df)
##   parameter true      mean     mode
## 1     beta1    2  2.083156  2.08338
## 2     beta2   -2 -1.920003 -1.91978

Fitting models with multiple likelihoods in inlabru

For this section recall the objects spde_model obtained above. Let us create a new data object. Observe that for inlabru we do not need to provide the covariates argument.

data_spde_bru <- graph_data_spde(graph_spde = spde_model, 
                name = "field", likelihood_col = "likelihood",
                resp_col = "y", loc_name = "loc")

We begin by loading inlabru library and setting up the likelihoods. To this end, we will use the first entry of data_spde_bru to supply the data for the first likelihood, and the second entry to supply the data for the second likelihood.

## Loading required package: fmesher
lik1 <- like(formula = y ~ intercept_1 + field,
            data=data_spde_bru[[1]][["data"]])
## Warning in bru_obs(formula = formula, family = family, data = data, response_data = response_data, : Non data-frame list-like data supplied; guessing allow_combine=TRUE.
##   Specify allow_combine explicitly to avoid this warning.
lik2 <- like(formula = y ~ intercept_2 + field,
            data=data_spde_bru[[2]][["data"]])            
## Warning in bru_obs(formula = formula, family = family, data = data, response_data = response_data, : Non data-frame list-like data supplied; guessing allow_combine=TRUE.
##   Specify allow_combine explicitly to avoid this warning.

Now, we create the model component:

cmp <-  ~ -1 + intercept_1(intercept_1) + 
        intercept_2(intercept_2) + 
        field(loc, model = spde_model)

Then, we fit the model:

spde_bru_fit <-  bru(cmp, lik1, lik2, 
                      options = list(num.threads = 1:1))

Let us now obtain the estimates in the original scale by using the spde_metric_graph_result() function, then taking a summary():

spde_bru_result <- spde_metric_graph_result(spde_bru_fit, "field", spde_model)

summary(spde_bru_result)
##           mean       sd 0.025quant 0.5quant 0.975quant     mode
## sigma 1.938400 0.175309  1.6214700  1.92738   2.312780 1.888540
## range 0.134569 0.027146  0.0905716  0.13128   0.196804 0.124566

We will now compare the means of the estimated values with the true values:

  result_bru_df <- data.frame(
    parameter = c("std.dev", "range"),
    true = c(sigma, r),
    mean = c(
      spde_bru_result$summary.sigma$mean,
      spde_bru_result$summary.range$mean
    ),
    mode = c(
      spde_bru_result$summary.sigma$mode,
      spde_bru_result$summary.range$mode
    )
  )
  print(result_bru_df)
##   parameter true      mean      mode
## 1   std.dev 2.00 1.9384013 1.8885448
## 2     range 0.15 0.1345693 0.1245663

Let us now look at the estimates of the measurement errors and compare with the true ones:

meas_err_bru_df <- data.frame(
    parameter = c("sigma1.e", "sigma2.e"),
    true = c(sigma1.e, sigma2.e),
    mean = sqrt(1/spde_bru_fit$summary.hyperpar$mean[1:2]),
    mode = sqrt(1/spde_bru_fit$summary.hyperpar$mode[1:2])
  )
print(meas_err_bru_df)
##   parameter true      mean      mode
## 1  sigma1.e  0.2 0.2232036 0.2378609
## 2  sigma2.e  0.5 0.4964284 0.4987477

Finally, let us look at the estimates of the intercepts:

intercept_df <- data.frame(
    parameter = c("beta1", "beta2"),
    true = c(beta1, beta2),
    mean = spde_bru_fit$summary.fixed$mean,
    mode = spde_bru_fit$summary.fixed$mode
  )
print(intercept_df)
##   parameter true      mean      mode
## 1     beta1    2  2.083163  2.083387
## 2     beta2   -2 -1.919996 -1.919774

A toy dataset with multiple likelihoods and replicates

Let us now proceed similarly, but now we will consider a case in which we have multiple likelihoods and replicates.

To simplify exposition, we will use the same base graph. So, we begin by clearing the observations.

graph$clear_observations()

We will use the same observation locations as for the previous cases. Let us sample 10 replicates:

sigma_rep <- 1.5
alpha_rep <- 1
nu_rep <- alpha_rep - 0.5
r_rep <- 0.2 # r stands for range
kappa_rep <- sqrt(8 * nu_rep) / r_rep

n_repl <- 10

u_rep <- sample_spde(range = r_rep, sigma = sigma_rep,
                 alpha = alpha_rep,
                 graph = graph, PtE = obs_loc,
                 nsim = n_repl)

Let us now generate the observed responses, which we will call y_rep.

beta1 = 2
beta2 = -2

sigma1.e <- 0.2
sigma2.e <- 0.5

n_obs_rep <- nrow(u_rep)

y1_rep <- beta1 + u_rep + sigma1.e * matrix(rnorm(n_obs_rep * n_repl),
                                    ncol=n_repl)     
y2_rep <- beta2 + u_rep + sigma2.e * matrix(rnorm(n_obs_rep * n_repl),
                                    ncol=n_repl)

Fitting the model with multiple likelihoods and replicates in R-INLA

The sample_spde() function returns a matrix in which each replicate is a column. We need to stack the columns together and a column to indicate the replicat. Further, we need to do it for each likelihood:

dl1_graph <- lapply(1:ncol(y1_rep), function(i){data.frame(y = y1_rep[,i],
                                          edge_number = obs_loc[,1],
                                          distance_on_edge = obs_loc[,2],
                                          likelihood = 1,
                                          intercept_1 = 1,
                                          intercept_2 = NA,
                                          repl = i)})
dl1_graph <- do.call(rbind, dl1_graph)

and

dl2_graph <- lapply(1:ncol(y2_rep), function(i){data.frame(y = y2_rep[,i],
                                          edge_number = obs_loc[,1],
                                          distance_on_edge = obs_loc[,2],
                                          likelihood = 2,
                                          intercept_1 = NA,
                                          intercept_2 = 1,
                                          repl = i)})
dl2_graph <- do.call(rbind, dl2_graph)

We now join them:

dl_graph <- rbind(dl1_graph, dl2_graph)

We can now add the the observations by setting the group argument to c("repl", "likelihood"):

graph$add_observations(data = dl_graph, normalized=TRUE, 
                            group = c("repl", "likelihood"),
                            edge_number = "edge_number",
                            distance_on_edge = "distance_on_edge")
## list()

Let us now create the model object:

spde_model_rep <- graph_spde(graph)

Let us first consider a case in which we do not use all replicates. Then, we consider the case in which we use all replicates.

Thus, let us assume we want only to consider replicates 1, 3, 5, 7 and 9. To this end, we the index object by using the graph_data_spde() function with the argument repl set to the replicates we want, in this case c(1,3,5,7,9). Observe that here we need to pass repl_col, as the internal grouping variable is not the replicate variable.

data_spde_repl <- graph_data_spde(graph_spde=spde_model_rep,
                      name="field", repl = c(1,3,5,7,9), repl_col = "repl", 
                      likelihood_col = "likelihood", resp_col = "y",
                      covariates = c("intercept_1", "intercept_2"))

Next, we create the stack objects, remembering that we need to input the components from data_spde for each likelihood:

stk_dat_rep1 <- inla.stack(data = data_spde_repl[[1]][["data"]], 
                        A = data_spde_repl[[1]][["basis"]], 
                        effects = data_spde_repl[[1]][["index"]]
    )
stk_dat_rep2 <- inla.stack(data = data_spde_repl[[2]][["data"]], 
                        A = data_spde_repl[[2]][["basis"]], 
                        effects = data_spde_repl[[2]][["index"]]
    )

stk_dat_rep <- inla.stack(stk_dat_rep1, stk_dat_rep2)

We now create the formula object, adding the name of the field (in our case field) attached with .repl a the replicate argument inside the f() function.

f_s_rep <- y ~ -1 + intercept_1 + intercept_2 + 
    f(field, model = spde_model_rep, 
        replicate = field.repl)

Then, we create the stack object with The inla.stack.data() function:

data_stk_rep <- inla.stack.data(stk_dat_rep)

Now, we fit the model:

spde_fit_rep <- inla(f_s_rep, family = c("gaussian", "gaussian"), 
                data = data_stk_rep, 
                control.predictor=list(A=inla.stack.A(stk_dat_rep)),
                               num.threads = "1:1")

Let us see the estimated values in the original scale:

spde_result_rep <- spde_metric_graph_result(spde_fit_rep, 
                        "field", spde_model_rep)

summary(spde_result_rep)
##           mean        sd 0.025quant 0.5quant 0.975quant     mode
## sigma 1.490520 0.0706553   1.361660 1.487580   1.638140 1.487760
## range 0.197119 0.0203377   0.161257 0.195638   0.241066 0.192024

Let us compare with the true values:

  result_df_rep <- data.frame(
    parameter = c("std.dev", "range"),
    true = c(sigma_rep, r_rep),
    mean = c(
      spde_result_rep$summary.sigma$mean,
      spde_result_rep$summary.range$mean
    ),
    mode = c(
      spde_result_rep$summary.sigma$mode,
      spde_result_rep$summary.range$mode
    )
  )
  print(result_df_rep)
##   parameter true      mean      mode
## 1   std.dev  1.5 1.4905218 1.4877614
## 2     range  0.2 0.1971192 0.1920243

Let us now look at the estimates of the measurement errors and compare with the true ones:

meas_err_df <- data.frame(
    parameter = c("sigma1.e", "sigma2.e"),
    true = c(sigma1.e, sigma2.e),
    mean = sqrt(1/spde_fit_rep$summary.hyperpar$mean[1:2]),
    mode = sqrt(1/spde_fit_rep$summary.hyperpar$mode[1:2])
  )
print(meas_err_df)
##   parameter true      mean      mode
## 1  sigma1.e  0.2 0.1934527 0.1946353
## 2  sigma2.e  0.5 0.4886221 0.4893065

Finally, let us look at the estimates of the intercepts:

intercept_df <- data.frame(
    parameter = c("beta1", "beta2"),
    true = c(beta1, beta2),
    mean = spde_fit_rep$summary.fixed$mean,
    mode = spde_fit_rep$summary.fixed$mode
  )
print(intercept_df)
##   parameter true      mean      mode
## 1     beta1    2  1.846520  1.846442
## 2     beta2   -2 -2.156769 -2.156847

Fitting models with multiple likelihoods and replicates in inlabru

For this section recall the objects spde_model_rep obtained above. Let us create a new data object:

data_spde_bru_repl <- graph_data_spde(graph_spde = spde_model_rep, 
                name="field", loc_name = "loc", 
                repl = c(1,3,5,7,9), repl_col = "repl", 
                likelihood_col = "likelihood", resp_col = "y")

Let us obtain the repl indexes from the data_spde_bru_repl object:

repl <- data_spde_bru_repl[["repl"]]

Let us now construct the likelihoods:

lik1_repl <- like(formula = y ~ intercept_1 + field,
            data=data_spde_bru_repl[[1]][["data"]])
## Warning in bru_obs(formula = formula, family = family, data = data, response_data = response_data, : Non data-frame list-like data supplied; guessing allow_combine=TRUE.
##   Specify allow_combine explicitly to avoid this warning.
lik2_repl <- like(formula = y ~ intercept_2 + field,
            data=data_spde_bru_repl[[2]][["data"]])            
## Warning in bru_obs(formula = formula, family = family, data = data, response_data = response_data, : Non data-frame list-like data supplied; guessing allow_combine=TRUE.
##   Specify allow_combine explicitly to avoid this warning.

Now, we create the model component, using the replicates index we obtained above:

cmp_repl <-  ~ -1 + intercept_1(intercept_1) + 
        intercept_2(intercept_2) + 
        field(loc, model = spde_model_rep, replicate = repl)

Then, we fit the model:

spde_bru_fit_repl <-  bru(cmp_repl, lik1_repl, lik2_repl,
                      options = list(num.threads = 1:1))

Let us now obtain the estimates in the original scale by using the spde_metric_graph_result() function, then taking a summary():

spde_bru_result_repl <- spde_metric_graph_result(spde_bru_fit_repl, "field", spde_model_rep)

summary(spde_bru_result_repl)
##           mean        sd 0.025quant 0.5quant 0.975quant     mode
## sigma 1.489950 0.0724681   1.354030 1.487450    1.64023 1.482510
## range 0.197383 0.0205611   0.160595 0.196124    0.24125 0.193441

We will now compare the means of the estimated values with the true values:

  result_bru_repl_df <- data.frame(
    parameter = c("std.dev", "range"),
    true = c(sigma_rep, r_rep),
    mean = c(
      spde_bru_result_repl$summary.sigma$mean,
      spde_bru_result_repl$summary.range$mean
    ),
    mode = c(
      spde_bru_result_repl$summary.sigma$mode,
      spde_bru_result_repl$summary.range$mode
    )
  )
  print(result_bru_repl_df)
##   parameter true      mean      mode
## 1   std.dev  1.5 1.4899496 1.4825101
## 2     range  0.2 0.1973831 0.1934412

Let us now look at the estimates of the measurement errors and compare with the true ones:

meas_err_bru_repl_df <- data.frame(
    parameter = c("sigma1.e", "sigma2.e"),
    true = c(sigma1.e, sigma2.e),
    mean = sqrt(1/spde_bru_fit_repl$summary.hyperpar$mean[1:2]),
    mode = sqrt(1/spde_bru_fit_repl$summary.hyperpar$mode[1:2])
  )
print(meas_err_bru_repl_df)
##   parameter true      mean      mode
## 1  sigma1.e  0.2 0.1935642 0.1949081
## 2  sigma2.e  0.5 0.4885810 0.4889947

Finally, let us look at the estimbates of the intercepts:

intercept_repl_df <- data.frame(
    parameter = c("beta1", "beta2"),
    true = c(beta1, beta2),
    mean = spde_bru_fit_repl$summary.fixed$mean,
    mode = spde_bru_fit_repl$summary.fixed$mode
  )
print(intercept_repl_df)
##   parameter true      mean      mode
## 1     beta1    2  1.846552  1.846472
## 2     beta2   -2 -2.156737 -2.156817