Skip to contents

Log-Gaussian Cox processes on metric graphs

David Bolin, Alexandre B. Simas

Created: 2023-01-30. Last modified: 2025-05-21.

Source: vignettes/pointprocess.Rmd
pointprocess.Rmd

Introduction

In this vignette we will introduce how to work with log-Gaussian Cox processes based on Whittle–Matérn fields on metric graphs. To simplify the integration with R-INLA and inlabru hese models are constructed using finite element approximations as implemented in the rSPDE package. The theoretical details will be given in the forthcoming article (Bolin, Simas, and Wallin 2023).

Constructing the graph and the mesh

We begin by loading the rSPDE, MetricGraph and INLA packages:

As an example, we consider the default graph in the package:

graph <- metric_graph$new(tolerance = list(vertex_vertex = 1e-1, vertex_edge = 1e-3, edge_edge = 1e-3),
                          remove_deg2 = TRUE)
graph$plot()

To construct a FEM approximation of a Whittle–Matérn field, we must first construct a mesh on the graph.

graph$build_mesh(h = 0.1)
graph$plot(mesh=TRUE)

The next step is to build the mass and stiffness matrices for the FEM basis.

  graph$compute_fem()

We are now ready to specify the and sample from a log-Gaussian Cox process model with intensity λ=exp(β+u)\lambda = \exp(\beta + u) where β\beta is an intercept and uu is a Gaussian Whittle–Matérn field specified by (κ2−Δ)α/2τu=𝒲. (\kappa^2 - \Delta)^{\alpha/2} \tau u = \mathcal{W}. For this we can use the function graph_lgcp as follows:

  sigma <- 0.5
  range <- 2
  alpha <- 2
  cov_lgcp <- graph$mesh$VtE[,1]/max(graph$mesh$VtE[,1])
  lgcp_sample <- graph_lgcp_sim(intercept = -1 + 2*cov_lgcp, sigma = sigma,
                            range = range, alpha = alpha,
                            graph = graph)

The object returned by the function is a list with the simulated Gaussian process and the points on the graph. We can plot the simulated intensity function as

graph$plot_function(X = exp(lgcp_sample$u), vertex_size = 0)

To plot the simulated points, we can add them to the graph and then plot:

graph$add_observations(data = data.frame(y=rep(1,length(lgcp_sample$edge_loc)),
                                         edge_number = lgcp_sample$edge_number,
                                         distance_on_edge = lgcp_sample$edge_loc,
                                         cov_lgcp = lgcp_sample$edge_number),
                       normalized = TRUE)
## Adding observations...
## Assuming the observations are normalized by the length of the edge.
graph$plot(vertex_size = 0, data = "y")

In order to fit a log-Gaussian Cox process model, we need to specify integration points on the graph, be able to evaluate the covariates at such integration points. This process is a bit involved, so we have created an interface to simplify the process. In this interface, by default, the covariates are interpolated from the data provided in the graph object to obtain their values at the integration points.

The integration points are defined, by default, as the mesh locations if the metric graph object has a mesh. If the mesh is not provided, one must either provide the integration points manually or build a mesh.

At the end of the vignette, we will also show how to fit the model in INLA without using our INLA interface for LGCP models.

Fitting LGCP models with our INLA interface

We will now fit the model using our INLA interface. To such an end, we will clear the observations from the graph and add the data to the graph.

graph$clear_observations()

#Add the data together with the exposure terms
graph$add_observations(data = data.frame(y = rep(1,length(lgcp_sample$edge_loc)),
                                         edge_number = lgcp_sample$edge_number,
                                         distance_on_edge = lgcp_sample$edge_loc,
                                         Intercept = 1,
                                         cov_lgcp = lgcp_sample$edge_number/max(lgcp_sample$edge_number)),
                       normalized = TRUE)
## Adding observations...
## Assuming the observations are normalized by the length of the edge.

We have added the response variable yy, however, this is not strictly necessary. If such a response variable is not provided, it will be assumed that all locations correspond to observed points.

Let us now create the rSPDE model object:

rspde_model <- rspde.metric_graph(graph, nu = alpha - 1/2)

We can now fit the model using the lgcp_graph() function:

inla_fit <- lgcp_graph(y ~ -1 + Intercept + cov_lgcp + 
                      f(field, model = rspde_model), graph=graph)

Let us observe the inla_fit object:

summary(inla_fit)
## Time used:
##     Pre = 2.06, Running = 0.552, Post = 0.0457, Total = 2.66 
## Fixed effects:
##             mean    sd 0.025quant 0.5quant 0.975quant   mode kld
## Intercept -0.545 0.331     -1.238   -0.533      0.071 -0.534   0
## cov_lgcp   0.976 0.491      0.030    0.969      1.964  0.969   0
## 
## Random effects:
##   Name     Model
##     field CGeneric
## 
## Model hyperparameters:
##                    mean    sd 0.025quant 0.5quant 0.975quant   mode
## Theta1 for field -0.832 0.394     -1.680   -0.807     -0.141 -0.686
## Theta2 for field  1.120 0.658     -0.174    1.119      2.418  1.116
## 
## Marginal log-Likelihood:  -109.72 
##  is computed 
## Posterior summaries for the linear predictor and the fitted values are computed
## (Posterior marginals needs also 'control.compute=list(return.marginals.predictor=TRUE)')

Let us extract the estimates in the original scale by using the spde_metric_graph_result() function, then taking a summary():

spde_result <- spde_metric_graph_result(inla_fit, "field", rspde_model)

summary(spde_result)
##             mean      sd 0.025quant 0.5quant 0.975quant     mode
## std.dev 0.468737 0.17586   0.188141 0.450051   0.864532 0.403134
## range   3.794120 2.73377   0.849470 3.061360  11.099200 1.991310

We will now compare the means of the estimated values with the true values:

  result_df <- data.frame(
    parameter = c("std.dev", "range"),
    true = c(sigma, range),
    mean = c(
      spde_result$summary.std.dev$mean,
      spde_result$summary.range$mean
    ),
    mode = c(
      spde_result$summary.std.dev$mode,
      spde_result$summary.range$mode
    )
  )
  print(result_df)
##   parameter true      mean      mode
## 1   std.dev  0.5 0.4687368 0.4031343
## 2     range  2.0 3.7941226 1.9913116

If we have the actual values of the covariates at the integration points, we can pass them to the lgcp_graph() function via the manual_covariates argument.

manual_covariates <- data.frame(Intercept = 1,
                      cov_lgcp = graph$mesh$VtE[,1]/max(lgcp_sample$edge_number),
                      .group = 1)
inla_fit <- lgcp_graph(y ~ -1 + Intercept + cov_lgcp + f(field, model = rspde_model), 
             graph=graph, manual_covariates = manual_covariates, interpolate = FALSE)

Let us observe the new inla_fit object:

summary(inla_fit)
## Time used:
##     Pre = 2.06, Running = 0.544, Post = 0.04, Total = 2.65 
## Fixed effects:
##             mean    sd 0.025quant 0.5quant 0.975quant   mode   kld
## Intercept -0.726 0.362     -1.499   -0.714     -0.037 -0.716 0.001
## cov_lgcp   1.424 0.412      0.628    1.420      2.247  1.420 0.000
## 
## Random effects:
##   Name     Model
##     field CGeneric
## 
## Model hyperparameters:
##                    mean    sd 0.025quant 0.5quant 0.975quant   mode
## Theta1 for field -0.866 0.417      -1.76    -0.84     -0.136 -0.712
## Theta2 for field  1.352 0.696       0.00     1.35      2.741  1.320
## 
## Marginal log-Likelihood:  -105.92 
##  is computed 
## Posterior summaries for the linear predictor and the fitted values are computed
## (Posterior marginals needs also 'control.compute=list(return.marginals.predictor=TRUE)')

We can now extract the estimates in the original scale

spde_result <- spde_metric_graph_result(inla_fit, "field", rspde_model)

summary(spde_result)
##            mean       sd 0.025quant 0.5quant 0.975quant    mode
## std.dev 0.45652 0.181032   0.172997 0.435522   0.868429 0.38128
## range   4.91905 3.849620   1.011020 3.835800  15.305900 2.37008

We can also plot the posterior marginal densities with the help of the gg_df() function:

  posterior_df_fit <- gg_df(spde_result)

  library(ggplot2)

  ggplot(posterior_df_fit) + geom_line(aes(x = x, y = y)) + 
  facet_wrap(~parameter, scales = "free") + labs(y = "Density")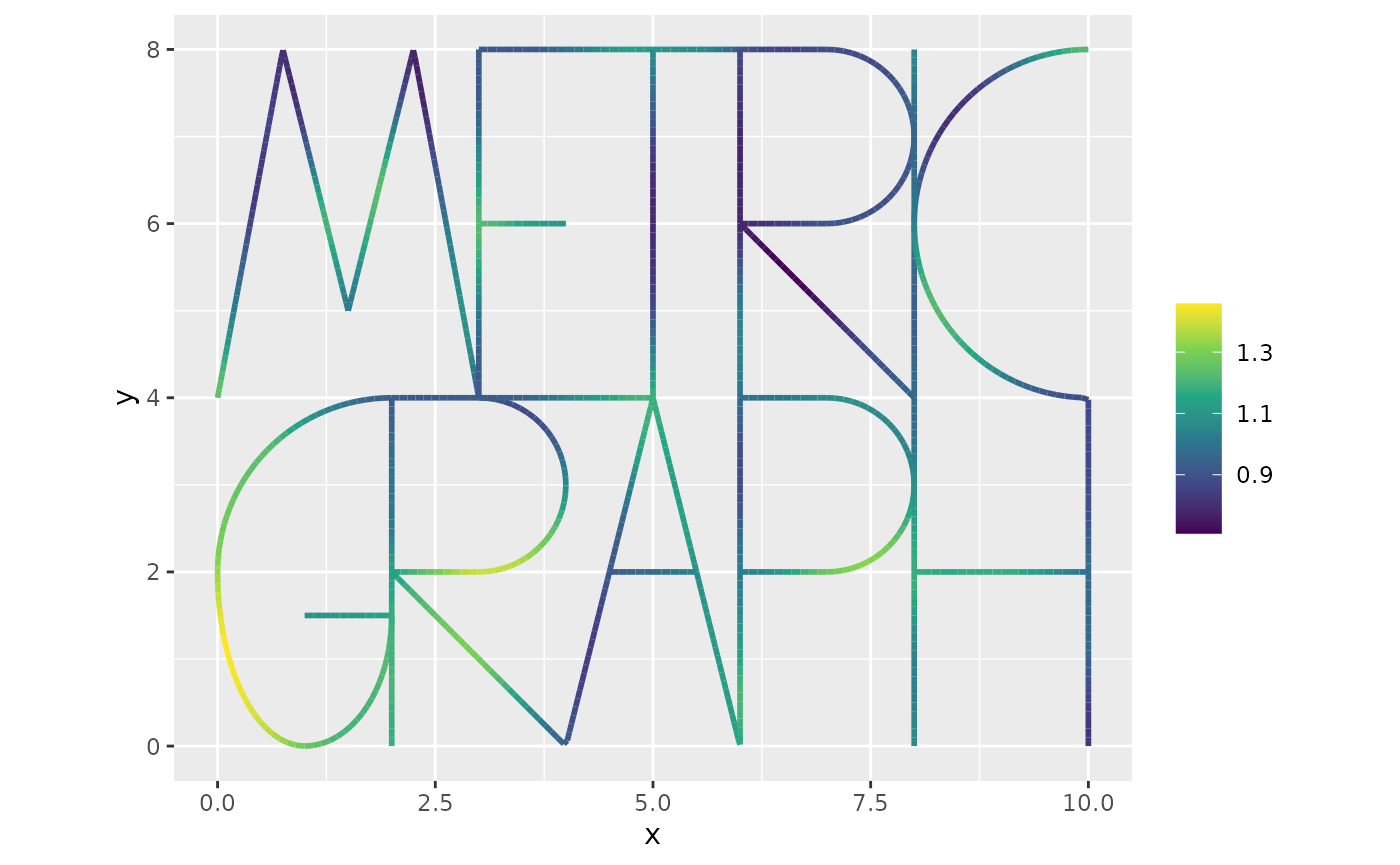

Finally, we can plot the estimated field uu:

n.obs <- length(graph$get_data()$y)
n.field <- dim(graph$mesh$VtE)[1]
u_posterior <- inla_fit$summary.linear.predictor$mean[(n.obs+1):(n.obs+n.field)]
graph$plot_function(X = u_posterior, vertex_size = 0)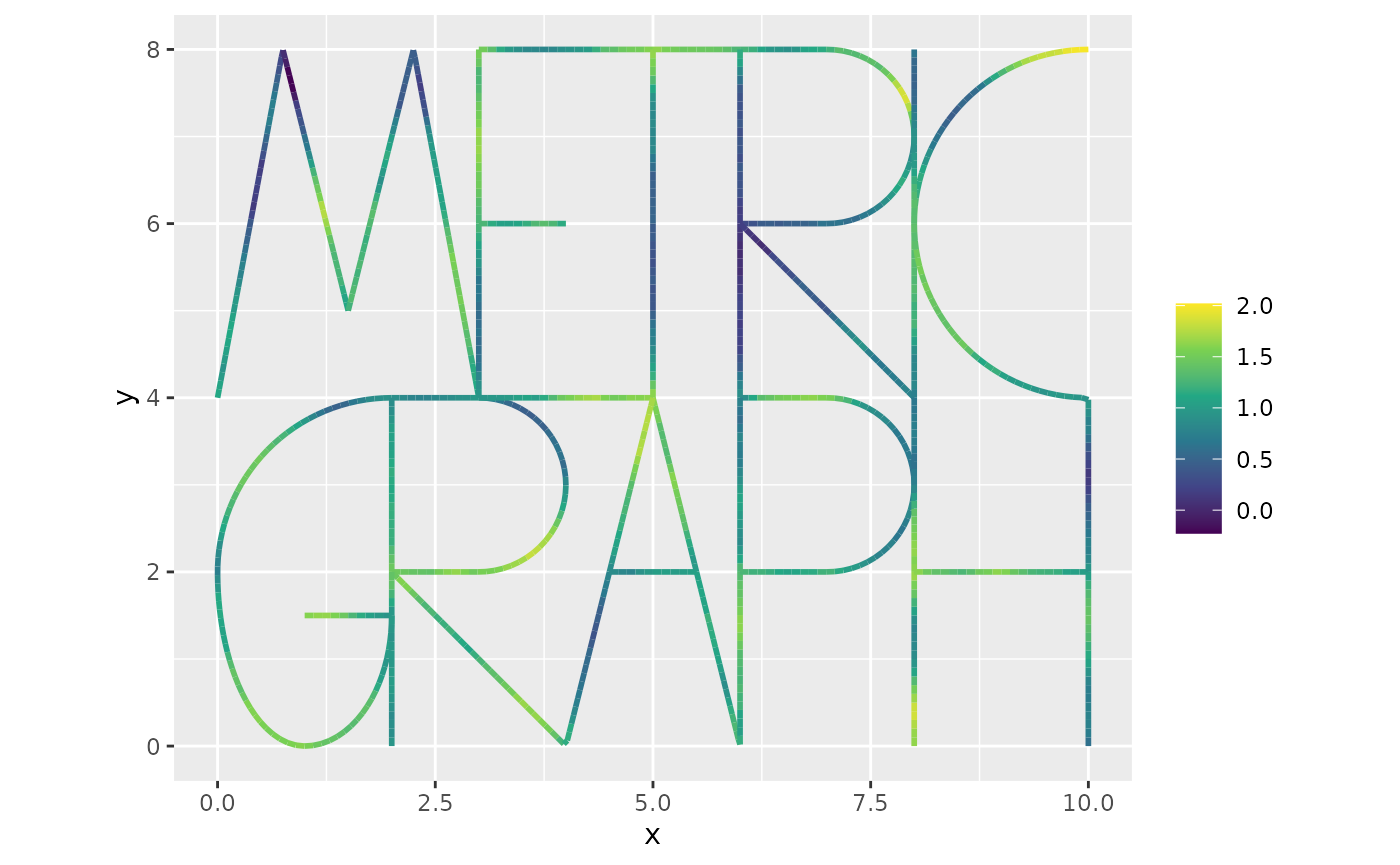

This can be compared with the field that was used to generate the data:

graph$plot_function(X = lgcp_sample$u, vertex_size = 0)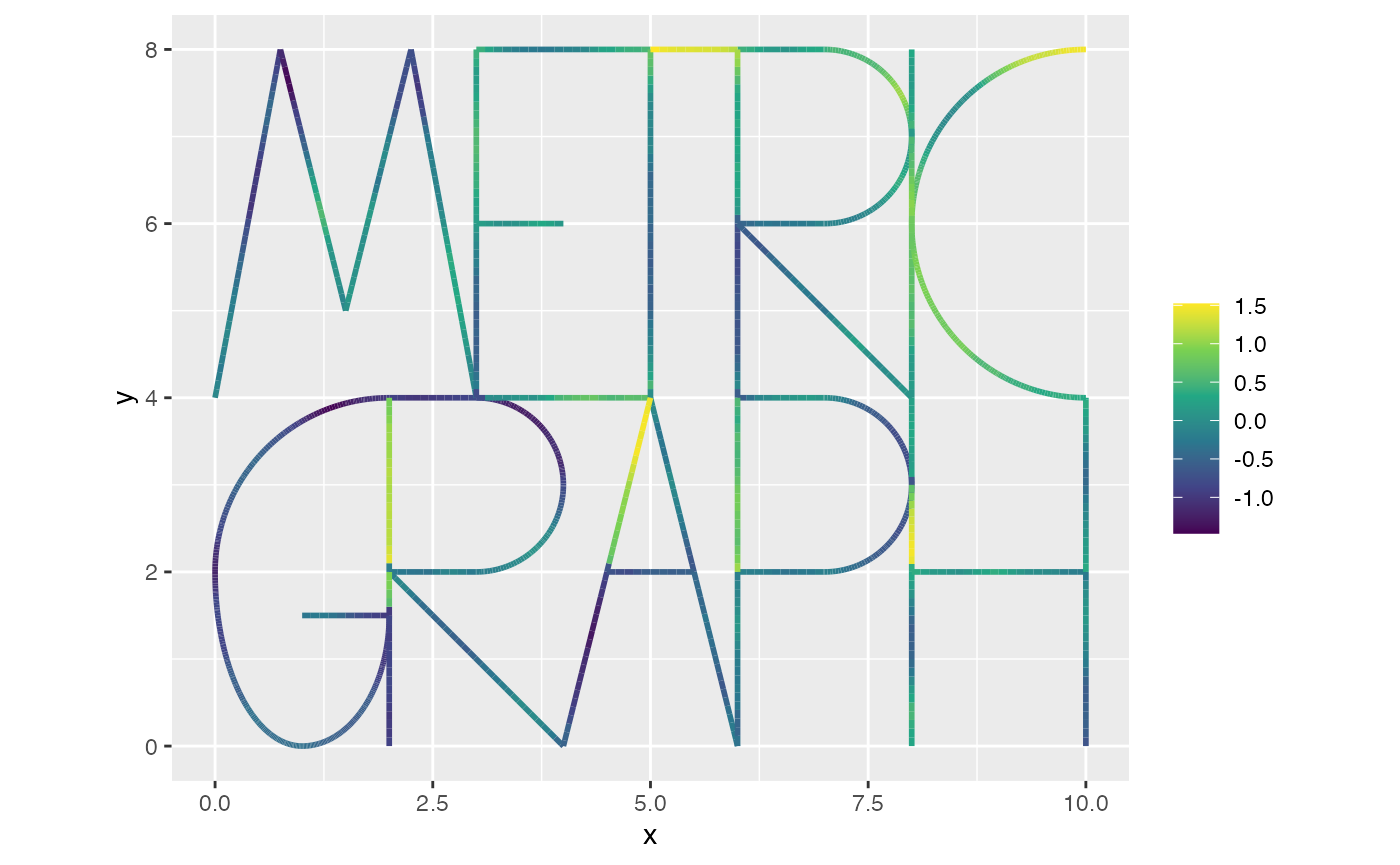

We can also fit the model using the exact model by using the graph_spde() function as the SPDE model:

spde_model <- graph_spde(graph, alpha = 1)

Let us now fit the model:

inla_fit_spde <- lgcp_graph(y ~ -1 + Intercept + cov_lgcp + 
                          f(field, model = spde_model), graph=graph)

Let us observe the new inla_fit_spde object:

summary(inla_fit_spde)
## Time used:
##     Pre = 1.76, Running = 0.525, Post = 0.0494, Total = 2.33 
## Fixed effects:
##             mean    sd 0.025quant 0.5quant 0.975quant   mode kld
## Intercept -0.551 0.336     -1.253   -0.539      0.077 -0.540   0
## cov_lgcp   0.961 0.487      0.026    0.953      1.944  0.953   0
## 
## Random effects:
##   Name     Model
##     field CGeneric
## 
## Model hyperparameters:
##                    mean    sd 0.025quant 0.5quant 0.975quant   mode
## Theta1 for field -0.654 0.548     -1.789   -0.635      0.366 -0.549
## Theta2 for field  1.343 0.922     -0.425    1.328      3.204  1.260
## 
## Marginal log-Likelihood:  -109.45 
##  is computed 
## Posterior summaries for the linear predictor and the fitted values are computed
## (Posterior marginals needs also 'control.compute=list(return.marginals.predictor=TRUE)')

We can now extract the estimates in the original scale

spde_result <- spde_metric_graph_result(inla_fit_spde, "field", spde_model)

summary(spde_result)
##          mean       sd 0.025quant 0.5quant 0.975quant     mode
## sigma 0.50432 0.200714   0.189121 0.480533   0.951447 0.397901
## range 5.87995 6.768320   0.663066 3.757220  24.215300 1.661400

An example with replicates in our INLA interface

We start by simulating the data.

  n.rep <- 30
  sigma <- 0.5
  range <- 2
  alpha <- 2
  cov_lgcp <- graph$mesh$VtE[,1]/max(graph$mesh$VtE[,1])  
  max_edge_num <- max(graph$mesh$VtE[,1])
  lgcp_sample_rep <- graph_lgcp_sim(n = n.rep, intercept = -1 + 2*cov_lgcp, sigma = sigma,
                            range = range, alpha = alpha,
                            graph = graph)

Let us clear the observations from the graph and add the simulated data.

graph$clear_observations()

df_rep <- data.frame(y=rep(1,length(lgcp_sample_rep[[1]]$edge_loc)),
                     edge_number = lgcp_sample_rep[[1]]$edge_number,
                     distance_on_edge = lgcp_sample_rep[[1]]$edge_loc,
                     Intercept = 1,
                     cov_lgcp = lgcp_sample_rep[[1]]$edge_number/max_edge_num,
                     rep = rep(1,length(lgcp_sample_rep[[1]]$edge_loc)))

for(i in 2:n.rep){
  df_rep <- rbind(df_rep, data.frame(y=rep(1,length(lgcp_sample_rep[[i]]$edge_loc)),
                                       edge_number = lgcp_sample_rep[[i]]$edge_number,
                                       distance_on_edge = lgcp_sample_rep[[i]]$edge_loc,
                                       Intercept = 1,
                                       cov_lgcp = lgcp_sample_rep[[i]]$edge_number/max_edge_num,
                                       rep = rep(i,length(lgcp_sample_rep[[i]]$edge_loc))))
}

graph$add_observations(data = df_rep,
                       normalized = TRUE,
                        group = "rep")
## Adding observations...
## Assuming the observations are normalized by the length of the edge.

Let us now fit the model. In this case, the default column for the replicates is .group, and also, by default, all replicates will be used.

inla_fit <- lgcp_graph(y ~ -1 + Intercept + cov_lgcp + f(field, model = rspde_model, replicate = field.repl), graph=graph)
## Warning in formula.character(object, env = baseenv()): Using formula(x) is deprecated when x is a character vector of length > 1.
##   Consider formula(paste(x, collapse = " ")) instead.

Let us observe the inla_fit object:

summary(inla_fit)
## Time used:
##     Pre = 2.13, Running = 25.4, Post = 1.1, Total = 28.7 
## Fixed effects:
##             mean    sd 0.025quant 0.5quant 0.975quant   mode kld
## Intercept -0.685 0.053     -0.789   -0.685     -0.581 -0.685   0
## cov_lgcp   1.221 0.083      1.057    1.221      1.384  1.221   0
## 
## Random effects:
##   Name     Model
##     field CGeneric
## 
## Model hyperparameters:
##                    mean    sd 0.025quant 0.5quant 0.975quant   mode
## Theta1 for field -0.481 0.046     -0.572   -0.481     -0.392 -0.480
## Theta2 for field  0.585 0.106      0.377    0.585      0.793  0.584
## 
## Marginal log-Likelihood:  -2658.04 
##  is computed 
## Posterior summaries for the linear predictor and the fitted values are computed
## (Posterior marginals needs also 'control.compute=list(return.marginals.predictor=TRUE)')

Let us now extract the estimates in the original scale

spde_result <- spde_metric_graph_result(inla_fit, "field", rspde_model)

summary(spde_result)
##             mean        sd 0.025quant 0.5quant 0.975quant     mode
## std.dev 0.618695 0.0280739   0.564892 0.618286   0.675097 0.617726
## range   1.804520 0.1900280   1.460460 1.794450   2.206100 1.773610

As in the previous case, we can also supply the covariates manually:

manual_covariates <- data.frame(
      Intercept = 1,
      cov_lgcp = rep(graph$mesh$VtE[,1]/max(graph$mesh$VtE[,1]), 30),
      .group = rep(1:30, each = nrow(graph$mesh$VtE))
    )
inla_fit <- lgcp_graph(y ~ -1 + Intercept + cov_lgcp + 
            f(field, model = rspde_model, replicate = field.repl), 
              graph=graph, manual_covariates = manual_covariates)
## Warning in formula.character(object, env = baseenv()): Using formula(x) is deprecated when x is a character vector of length > 1.
##   Consider formula(paste(x, collapse = " ")) instead.

Let us observe the inla_fit object:

summary(inla_fit)
## Time used:
##     Pre = 1.9, Running = 25.2, Post = 1.19, Total = 28.2 
## Fixed effects:
##             mean    sd 0.025quant 0.5quant 0.975quant   mode kld
## Intercept -0.931 0.049     -1.026   -0.930     -0.836 -0.930   0
## cov_lgcp   1.866 0.075      1.718    1.865      2.013  1.865   0
## 
## Random effects:
##   Name     Model
##     field CGeneric
## 
## Model hyperparameters:
##                    mean    sd 0.025quant 0.5quant 0.975quant   mode
## Theta1 for field -0.655 0.057     -0.768   -0.654     -0.545 -0.652
## Theta2 for field  0.591 0.131      0.334    0.590      0.850  0.588
## 
## Marginal log-Likelihood:  -2472.17 
##  is computed 
## Posterior summaries for the linear predictor and the fitted values are computed
## (Posterior marginals needs also 'control.compute=list(return.marginals.predictor=TRUE)')

Let us now extract the estimates in the original scale

spde_result <- spde_metric_graph_result(inla_fit, "field", rspde_model)

summary(spde_result)
##             mean        sd 0.025quant 0.5quant 0.975quant     mode
## std.dev 0.520492 0.0293267   0.464441 0.520035   0.579539 0.519559
## range   1.820460 0.2384790   1.399000 1.804160   2.334290 1.771910

Fitting LGCP models without our INLA interface

We are now in a position to fit the model with our R-INLA implementation, without using our INLA interface for LGCP models. When working with log-Gaussian Cox processes, the likelihood has a term ∫Γexp(u(s))ds\int_\Gamma \exp(u(s)) ds that needs to be handled separately. This is done by using the mid-point rule as suggested for SPDE models by Simpson et al. (2016) where we approximate ∫Γexp(u(s))ds≈∑i=1pãiexp(u(s̃i)). \int_\Gamma \exp(u(s)) ds \approx \sum_{i=1}^p \widetilde{a}_i \exp\left(u(\widetilde{s}_i)\right). Using the fact that u(s)=∑j=1nφ(s)uiu(s) = \sum_{j=1}^n \varphi(s) u_i from the FEM approximation, we can write the integral as α̃Texp(Ãu)\widetilde{\alpha}^T\exp(\widetilde{A}u) where Ãij=φj(s̃i)\widetilde{A}_{ij} = \varphi_j(\widetilde{s}_i) and ã\widetilde{a} is a vector with integration weights. These quantities can be obtained as

Atilde <- graph$fem_basis(graph$mesh$VtE)
atilde <- graph$mesh$weights

The weights are used as exposure terms in the Poisson likelihiood in R-INLA. Because of this, the easiest way to construct the model is to add the integration points as zero observations in the graph, with corresponding exposure weights. We also need to add the exposure terms (which are zero) for the actual observation locations:

#clear the previous data in the graph
graph$clear_observations()

#Add the data together with the exposure terms
graph$add_observations(data = data.frame(y = rep(1,length(lgcp_sample$edge_loc)),
                                         e = rep(0,length(lgcp_sample$edge_loc)),
                                         edge_number = lgcp_sample$edge_number,
                                         distance_on_edge = lgcp_sample$edge_loc,
                                         Intercept = 1,
                                         cov_lgcp = lgcp_sample$edge_number/max(lgcp_sample$edge_number)),
                       normalized = TRUE)
## Adding observations...
## Assuming the observations are normalized by the length of the edge.
#Add integration points
graph$add_observations(data = data.frame(y = rep(0,length(atilde)),
                                         e = atilde,
                                         edge_number = graph$mesh$VtE[,1],
                                         distance_on_edge = graph$mesh$VtE[,2],
                                         Intercept = 1,
                                         cov_lgcp = graph$mesh$VtE[,1]/max(lgcp_sample$edge_number)),
                       normalized = TRUE)
## Adding observations...
## Assuming the observations are normalized by the length of the edge.

We now create the inla model object with the graph_spde function. For simplicity, we assume that α\alpha is known and fixed to the true value in the model.

rspde_model <- rspde.metric_graph(graph, nu = alpha - 1/2)

Next, we compute the auxiliary data:

data_rspde <- graph_data_spde(rspde_model, name="field", covariates = c("Intercept","cov_lgcp"))

We now create the inla.stack object with the inla.stack() function. At this stage, it is important that the data has been added to the graph since it is supplied to the stack by using the graph_spde_data() function.

stk <- inla.stack(data = data_rspde[["data"]], 
                  A = data_rspde[["basis"]],
                  effects = data_rspde[["index"]])

We can now fit the model using R-INLA:

spde_fit <- inla(y ~ -1 + Intercept + cov_lgcp + f(field, model = rspde_model), 
                 family = "poisson", data = inla.stack.data(stk),
                 control.predictor = list(A = inla.stack.A(stk), compute = TRUE),
                 E = inla.stack.data(stk)$e)

Let us extract the estimates in the original scale by using the spde_metric_graph_result() function, then taking a summary():

spde_result <- rspde.result(spde_fit, "field", rspde_model)

summary(spde_result)
##            mean       sd 0.025quant 0.5quant 0.975quant    mode
## std.dev 0.45652 0.181032   0.172996 0.435521    0.86843 0.38128
## range   4.91904 3.849600   1.011020 3.835800   15.30590 2.37008

We will now compare the means of the estimated values with the true values:

  result_df <- data.frame(
    parameter = c("std.dev", "range"),
    true = c(sigma, range),
    mean = c(
      spde_result$summary.std.dev$mean,
      spde_result$summary.range$mean
    ),
    mode = c(
      spde_result$summary.std.dev$mode,
      spde_result$summary.range$mode
    )
  )
  print(result_df)
##   parameter true      mean     mode
## 1   std.dev  0.5 0.4565199 0.381280
## 2     range  2.0 4.9190434 2.370085

An example with replicates

We now clear the previous data and add the new data together with the exposure terms

  graph$clear_observations()
  df_rep <- data.frame(y=rep(1,length(lgcp_sample_rep[[1]]$edge_loc)),
                                             e = rep(0,length(lgcp_sample_rep[[1]]$edge_loc)),
                                         edge_number = lgcp_sample_rep[[1]]$edge_number,
                                         distance_on_edge = lgcp_sample_rep[[1]]$edge_loc,
                                         Intercept = 1,
                                         cov_lgcp = lgcp_sample_rep[[1]]$edge_number/max_edge_num,
                                         rep = rep(1,length(lgcp_sample_rep[[1]]$edge_loc)))

  df_rep <- rbind(df_rep, data.frame(y = rep(0,length(atilde)),
                                         e = atilde,
                                         edge_number = graph$mesh$VtE[,1],
                                         distance_on_edge = graph$mesh$VtE[,2],
                                         Intercept = 1,
                                         cov_lgcp = graph$mesh$VtE[,1]/max_edge_num,
                                         rep = rep(1,length(atilde))))
  for(i in 2:n.rep){
    df_rep <- rbind(df_rep, data.frame(y=rep(1,length(lgcp_sample_rep[[i]]$edge_loc)),
                                             e = rep(0,length(lgcp_sample_rep[[i]]$edge_loc)),
                                         edge_number = lgcp_sample_rep[[i]]$edge_number,
                                         distance_on_edge = lgcp_sample_rep[[i]]$edge_loc,
                                         Intercept = 1,
                                         cov_lgcp = lgcp_sample_rep[[i]]$edge_number/max_edge_num,
                                         rep = rep(i,length(lgcp_sample_rep[[i]]$edge_loc))))
    df_rep <- rbind(df_rep, data.frame(y = rep(0,length(atilde)),
                                         e = atilde,
                                         edge_number = graph$mesh$VtE[,1],
                                         distance_on_edge = graph$mesh$VtE[,2],
                                         Intercept = 1,
                                         cov_lgcp = graph$mesh$VtE[,1]/max_edge_num,
                                         rep = rep(i,length(atilde))))                                        

  }

      graph$add_observations(data = df_rep,
                       normalized = TRUE,
                        group = "rep")
## Adding observations...
## Assuming the observations are normalized by the length of the edge.

We can now define and fit the model as previously

rspde_model <- rspde.metric_graph(graph, nu = alpha - 1/2)

data_rspde <- graph_data_spde(rspde_model, name = "field", 
                                  repl = ".all", repl_col = "rep", 
                                  covariates = c("Intercept","cov_lgcp"))

stk <- inla.stack(data = data_rspde[["data"]], 
                  A = data_rspde[["basis"]], 
                  effects = data_rspde[["index"]])

spde_fit <- inla(y ~ -1 + Intercept + cov_lgcp + 
                 f(field, model = rspde_model, replicate = field.repl), 
                 family = "poisson", data = inla.stack.data(stk),
                 control.predictor = list(A = inla.stack.A(stk), compute = TRUE),
                 E = inla.stack.data(stk)$e)

Let’s look at the summaries

spde_result <- rspde.result(spde_fit, "field", rspde_model)
summary(spde_result)
##             mean        sd 0.025quant 0.5quant 0.975quant     mode
## std.dev 0.520491 0.0293267   0.464441 0.520035   0.579539 0.519558
## range   1.820460 0.2384790   1.399000 1.804160   2.334290 1.771910
result_df <- data.frame(
    parameter = c("std.dev", "range"),
    true = c(sigma, range),
    mean = c(
      spde_result$summary.std.dev$mean,
      spde_result$summary.range$mean
    ),
    mode = c(
      spde_result$summary.std.dev$mode,
      spde_result$summary.range$mode
    )
  )
  print(result_df)
##   parameter true      mean      mode
## 1   std.dev  0.5 0.5204915 0.5195585
## 2     range  2.0 1.8204601 1.7719073

References

Bolin, David, Alexandre B. Simas, and Jonas Wallin. 2023. “Log-Cox Gaussian Processes and Space-Time Models on Compact Metric Graphs.” In Preparation.
Simpson, Daniel, Janine B. Illian, Finn Lindgren, Siv H. Sørbye, and Håvard Rue. 2016. “Going Off Grid: Computationally Efficient Inference for Log-Gaussian Cox Processes.” Biometrika.